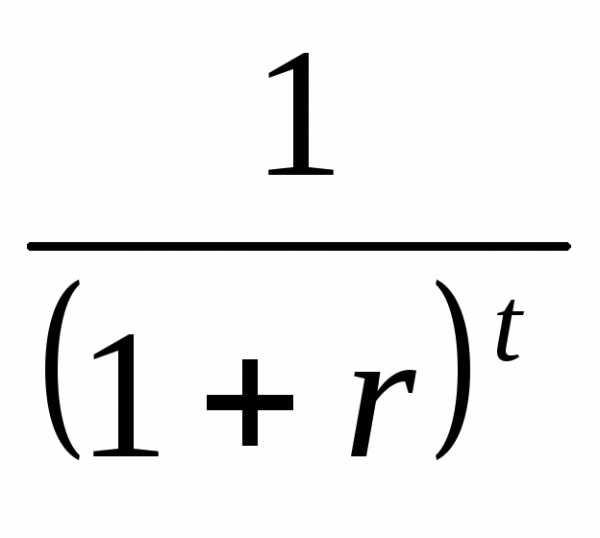Внутренняя норма рентабельности

Содержание

Внутренняя норма доходности. Формула и пример расчета в Excel

Разберем такой показатель как внутренняя норма доходности инвестиционного проекта, определим экономический смысл и рассмотрим подробно пример его расчета с помощью Excel.

Внутренняя норма доходности инвестиционного проекта (IRR). Определение

Внутренняя норма доходности (англ. Internal Rate of Return, IRR, внутренняя норма прибыли, внутренняя норма, внутренняя норма рентабельности, внутренняя норма дисконта, внутренний коэффициент эффективности, внутренний коэффициент окупаемости) – коэффициент, показывающий максимально допустимый риск по инвестиционному проекту или минимальный приемлемый уровень доходности. Внутренняя норма доходности равна ставке дисконтирования, при которой чистый дисконтированный доход отсутствует, то есть равен нулю.

★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут

Внутренняя норма доходности формула расчета

где:

CF_t (Cash Flow) – денежный поток в период времени t;

IC (Invest

Capital) – инвестиционные затраты на проект в первоначальном периоде (тоже являются денежным потоком CF₀ = IC).

t – период времени.

Применение внутренней нормы доходности

Показатель используется для оценки привлекательности инвестиционного проекта или для сопоставительного анализа с другими проектами. Для этого IRR сравнивают с эффективной ставкой дисконтирования, то есть с требуемым уровнем доходности проекта (r). За такой уровень на практике зачастую используют средневзвешенную стоимость капитала (Weight Average Cost of Capital, WACC).

Значение IRR	Комментарии
IRR>WACC	Инвестиционный проект имеет внутреннюю норму доходности выше чем затраты на собственный и заемный капитал. Данный проект следует принять для дальнейшего анализа
IRR<WACC	Инвестиционный проект имеет норму доходности ниже чем затраты на капитал, это свидетельствует о нецелесообразности вложения в него
IRR=WACC	Внутренняя доходность проекта равна стоимости капитала, проект находится на минимально допустимом уровне и следует произвести корректировки движения денежных средств и увеличить денежные потоки
IRR₁>IRR₂	Инвестиционный проект (1) имеет больший потенциал для вложения чем (2)

Следует заметить, что вместо критерия сравнения WACC может быть любой другой барьерный уровень инвестиционных затрат, который может быть рассчитан по методам оценки ставки дисконтирования. Данные методы подробно рассмотрены в статье «Ставка дисконтирования. 10 современных методов расчета». Простым практическим примером, может быть сравнение IRR с безрисковой процентной ставкой по банковскому вкладу. Так если инвестиционный проект имеет IRR=10%, а процент по вкладу=16%, то данный проект следует отклонить.

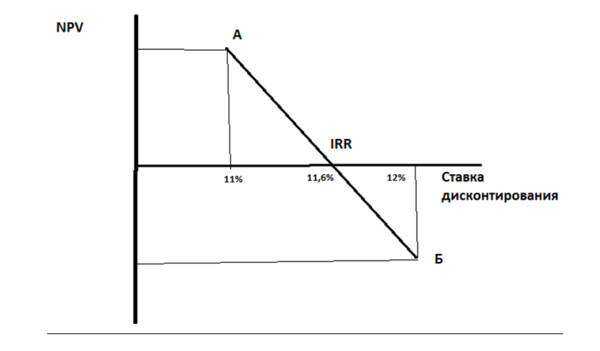
Внутренняя норма доходности (IRR) тесно связана с чистым дисконтированным доходном (NPV). На рисунке ниже показана взаимосвязь между размером IRR и NPV, увеличение нормы доходности приводит к уменьшению дохода от инвестиционного проекта.

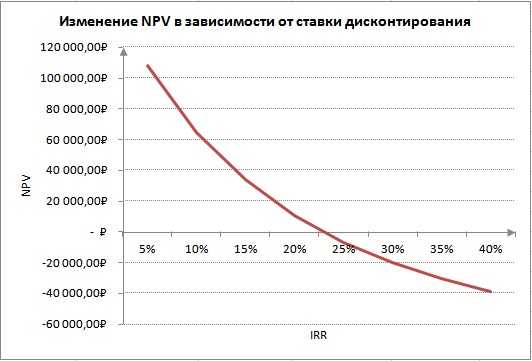
Изменение чистого дисконтированного дохода в зависимости от внутренней нормы доходности

Внутренняя норма доходности занимает второе место в инвестиционном анализе проектов, другие показатели оценки проектов более подробно рассмотрены в статье: «6 методов оценки эффективности инвестиций в Excel. Пример расчета NPV, PP, DPP, IRR, ARR, PI«.

Мастер-класс: «Как рассчитать внутреннюю норму доходности бизнес плана»

Расчет внутренней нормы доходности (IRR) на примере в Excel

Рассмотрим пример расчета внутренней нормы доходности на примере с помощью Excel, разберем два способа построения с помощью функции и с помощью надстройки «Поиск решений».

Пример расчета IRR в Excel c помощью встроенной функции

В программе есть встроенная финансовая функция, позволяющая быстро произвести расчет данного показателя – ВСД (внутренняя ставка дисконта). Следует заметить, что данная формула будет работать только тогда, когда есть хотя бы один положительный и один отрицательный денежный поток. Формула расчета в Excel будет иметь следующий вид:

Внутренняя норма доходности (E16) =ВСД(E6:E15)

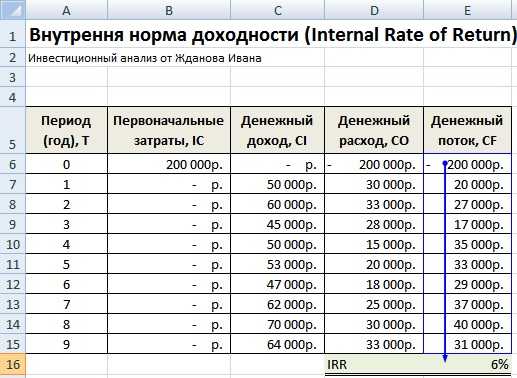
Внутренняя норма доходности. Расчет в Excel по встроенной формуле

В результате мы получили, что внутренняя норма доходности равняется 6%, далее для проведения инвестиционного анализа, полученное значение необходимо сопоставить со стоимостью капитала (WACC) данного проекта.

Пример расчета IRR через надстройку «Поиск решений»

Второй вариант расчета подразумевает использование надстройки «Поиск решений» для поиска оптимального значения ставки дисконтирования для NPV=0. Для этого необходимо рассчитать чистый дисконтированный доход (NPV).

На рисунке ниже показаны формулы расчета дисконтированного денежного потока по годам, сумма которых дает чистый дисконтированный доход. Формула расчета дисконтированного денежного потока (DCF) следующая:

Дисконтированный денежный поток (F) =E7/(1+$F$17)^A7

Чистый дисконтированный доход (NPV) =СУММ(F7:F15)-B6

На рисунке ниже показан первоначальный вид для расчета IRR. Можно заметить, что ставка дисконтирования, используемая для расчета NPV, ссылается на ячейку, в которой нет данных (она принимается равной 0).

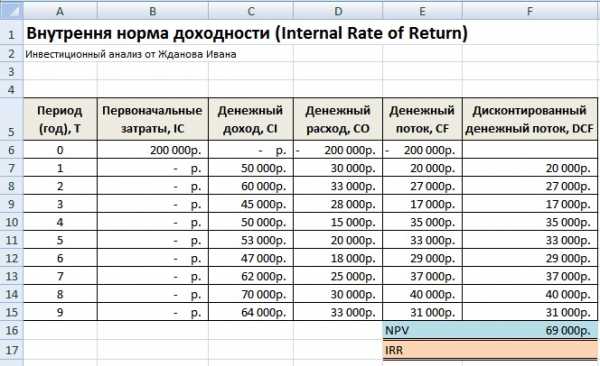
Внутренняя норма доходности (IRR) и NPV. Расчет в Excel в помощью надстройки

Сейчас наша задача состоит в том, чтобы отыскать на основе оптимизации с помощью надстройки «Поиск решений», то значение ставки дисконтирования (IRR) при котором NPV проекта будет равен нулю. Для этого открываем в главном меню раздел «Данные» и в нем «Поиск решений».

При нажатии в появившемся окне заполняем строки «Установить целевую ячейку» – это формула расчета NPV, далее выбираем значение данной ячейки равной 0. Изменяемый параметр будет ячейка со значением внутренней нормы доходности (IRR). На рисунке ниже показан пример расчета с помощью надстройки «Поиск решений».

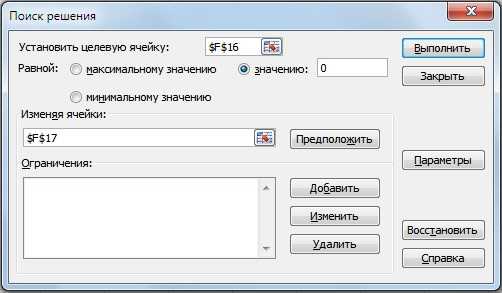
Поиск значения IRR для NPV=0

После оптимизации программа заполнит нашу пустую ячейку (F17) значением ставки дисконтирования, при которой чистый дисконтированный доход равен нулю. В нашем случае получилось 6%, результат полностью совпадает с расчетом по строенной формуле в Excel.

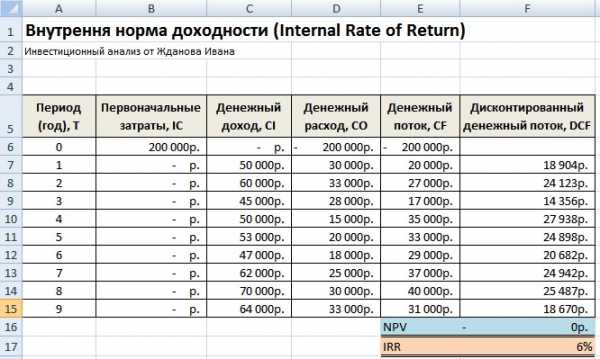
Результат расчета внутренней нормы доходности (IRR)

Расчет внутренней нормы доходности в Excel для несистематических поступлений

На практике часто случается, что денежные средства поступают не периодично. В результате ставка дисконтирования для каждого денежного потока будет меняться, это делает невозможным использовать формулу ВСД в Excel. Для решения данной задачи используется другая финансовая формула ЧИСТВНДОХ (). Данная формула включает в себя массив дат и денежные потоки. Формула расчета будет иметь следующий вид:

=ЧИСТВНДОХ(E6:E15;A6:A15;0)

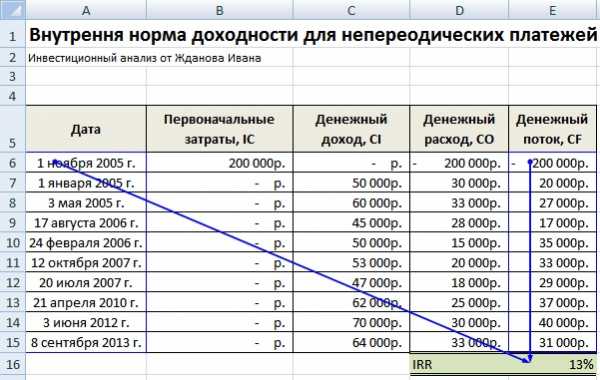
Расчет внутренней нормы доходности в Excel для несистематических платежей

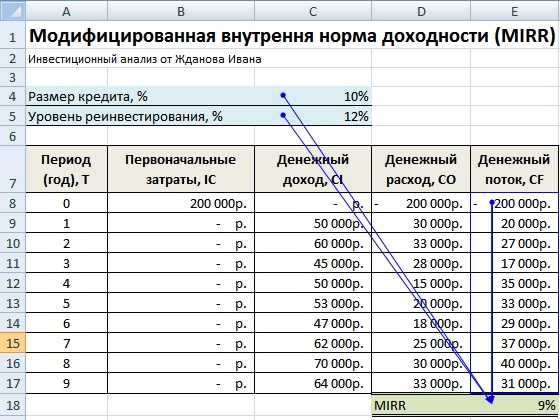
Модифицированная внутренняя норма доходности (MIRR)

В инвестиционном анализе также используется модифицированная внутренняя норма доходности (Modified Internal Rate of Return, MIRR) – данный показатель отражает минимальный внутренний уровень доходности проекта при осуществлении реинвестиций в проект. Данный проект использует процентные ставки, полученные от реинвестирования капитала. Формула расчета модифицированной внутренней нормы доходности следующая:

где:

MIRR – внутренняя норма доходности инвестиционного проекта;

COF_t – отток денежных средств в периоды времени t;

CIFt – приток денежных средств;

r – ставка дисконтирования, которая может рассчитываться как средневзвешенная стоимость капитала WACC;

d – процентная ставка реинвестирования капитала;

n – количество временных периодов.

Расчет модифицированной внутренней нормы доходности в Excel

Для расчета данной модификации внутренней нормы прибыльности можно воспользоваться встроенной функцией Excel, которая использует помимо денежных потоков еще размер ставки дисконтирования и уровень доходности при реинвестировании. Формула расчета показателя представлена ниже:

MIRR =МВСД(E8:E17;C4;C5)

Преимущества и недостатки внутренней нормы доходности (IRR)

Рассмотрим преимущества показателя внутренней нормы доходности для оценки проектов.

Во-первых, возможность сравнения различных инвестиционных проектов между собой по степени привлекательности и эффективности использования капитала. К примеру, сравнение с доходностью по безрисковым активам.

Во-вторых, возможность сравнения различных инвестиционных проектов с разным горизонтом инвестирования.

К недостаткам показателя относят:

Во-первых, недостатки в оценке внутренней нормы доходности заключаются в сложности прогнозирования будущих денежных платежей. На размер планируемых платежей влияет множество факторов риска, влияние которые сложно объективно оценить.

Во-вторых, показатель IRR не отражает размер реинвестирования в проект (данный недостаток решен в модифицированной внутренней норме доходности MIRR).

В-третьих, не способность отразить абсолютный размер полученных денежных средств от инвестиции.

★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут

Резюме

В данной статье мы рассмотрели формулу расчета внутренней нормы доходности (IRR), разобрали подробно два способа построения данного инвестиционного показателя с помощью Excel: на основе встроенных функций и надстройки «Поиск решений» для систематических и несистематических денежных потоков. Выделили, что внутренняя норма доходности является вторым по значимости показателем оценки инвестиционных проектов после чистого дисконтированного дохода (NPV). Вариацией IRR является ее модификация MIRR, которая учитывает также доходность от реинвестирования капитала.

Автор: к.э.н. Жданов Иван Юрьевич

finzz.ru

13.3.2 Внутренняя норма доходности (внд)

Внутренняя норма доходности (ВНД) (IRR – internal rate of return) это ставка дисконта, при которой чистая приведенная стоимость (ЧПС) равна нулю, т.е. в общем случае решением следующего уравнения

Внутренняя норма доходности (ВНД) – это собственная доходность, присущая проекту и обусловленная денежными потоками. И, если она (В НД) больше стоимости капитала фирмы, т.е. требуемой нормы доходности, то проект приемлем для фирмы, если же меньше – не приемлем.

Для инвестиционных проектов, подобных проекту приобретения новой техники, который рассматриваем и денежные потоки у которого неравномерны по периодам, определение ВНД производится методом последовательного приближения.

Процедура расчета ВНД следующая:

Дисконтировать потоки денег по ставке , равной стоимости капитала фирмы;
Если полученная при этом чистая приведенная стоимость (ЧПС) положительна, то увеличить ставку дисконтирования с тем, чтобы получить отрицательное значение ЧПС;
Если же она отрицательна, то уменьшить ставку дисконтирования, чтобы получить положительные значения ЧПС;
Повторять пункты 2 и 3 до тех пор, пока не получим нулевое значение ЧПС.

Рассмотрим эту процедуру на примере проекта приобретения новой техники. Из предыдущих расчетов известно, что при ставке 15% (r = 0,15), равной стоимости капитала фирмы, величина ЧПС равна 3388 д.е.

Дальнейшие расчеты сведены в таблицу 12.2

Таблица 12.2 Расчет ВНД

годы	Денежный поток	r = 15%		r = 20%		r = 18%		r = 19%
годы	Денежный поток		PV		PV		PV		PV
1	13000	0,870	11310	0,833	10830	0,848	11020	0,840	10920
2	15000	0,756	11340	0,694	10410	0,718	10770	0,706	10590
3	15000	0,658	9870	0,579	8680	0,609	9140	0,593	8890
4	19000	0,572	10868	0,482	9160	0,516	9800	0,499	9480
∑PV			43388		39080		40730		39880
КВ			-40000		-40000		-40000		-40000
ЧПС			+3388		-920		+730		-120

Как видно из таблицы ВНД находится между 18% и 19%. Дальнейшее уточнение произведем с помощью аппроксимирующей формулы

где: r₁ – значение дисконта, при котором ЧПС > 0;

r_r– значение дисконта, при котором ЧПС < 0;

f(r₁) – значение чпс при r₁;

f(r_r) – значение ЧПС при r_r_/

Подставив полученные значения при r = 18% и r = 19%, получим

Так как полученное значение ВНД, равное 18,86%, больше, чем требуемое фирмой 15%, то рассматриваемый проект приобретения новой техники приемлем.

На рис.12.3 показана взаимосвязь между чистой приведенной стоимостью (ЧПС) и внутренней нормой доходности (ВНД). Функция ЧПС (r) является убывающей функцией и точка пересечения с осью абсцисс показывает внутреннюю норму доходности (рис.12.3а).

С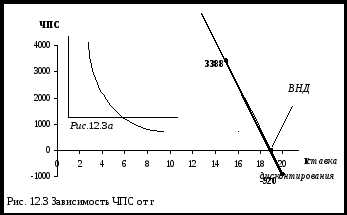ледует здесь сделать ряд замечаний:

При всей своей очевидной сложности, вычисление ВНД по вышеизложенной методике дает лишь приблизительные результаты, в основном из-за нелинейности функции ЧПС от коэффициента дисконтирования;
Критерий внутренняя норма доходности таит в себе некоторые сложности из-за возможности иметь несколько корней, из-за возможности возрастания функции ЧПС от увеличения дисконта (ставки процента) и других причин;
Необходимо четко понимать понятие внутренняя норма доходности и альтернативные издержки т.к. оба эти понятия выступают в качестве ставки дисконта при определении чистой приведенной стоимости. Внутренняя норма доходности является измерителем рентабельности, которая зависит исключительно от величины и времени возникновения потока денежных средств проекта. Альтернативные издержки представляют собой критерий рентабельности, который используется для того, чтобы определить, сколько стоит проект. Величина альтернативных издержек устанавливается на рынке капитала и представляет собой ожидаемую норму доходности других активов, риск которых сопоставим с риском оцениваемого проекта;
Несмотря на частое использование внутренняя норма доходности при анализе о оценке инвестиционных проектов, ВНД – это произвольная величина без какого-либо элементарного экономического смысла. Это просто ставка дисконта, при которой чистая приведенная стоимость всех потоков денежных средств проекта равна нулю. ВНД представляет собой сложную среднюю отдельных процентных ставок. ВНД – сама по себе очень полезна.

Окупаемость

Было уже рассмотрено период окупаемости, традиционный метод его расчета и некоторые недостатки. Здесь рассмотрим правило дисконтированной окупаемости, которое можно перефразировать вопросом: «в течение какого периода должен реализоваться проект, чтобы он имел смысл с точки зрения чистой приведенной стоимости». Эта модификация принципа окупаемости позволяет избежать ошибок, связанных с единообразной оценкой потоков денежных средств, возникающих за время периода окупаемости

Предположим, имеется три взаимоисключающих проекта. Исходные данные и результаты расчета приведены в таблице 12.3.

Традиционный метод расчета дает одинаковую оценку периода окупаемости у всех трех проектов, равный 3 годам.

Таблица 12.3 Расчет дисконтированного периода окупаемости

годы	Коэффициент дисконтирова- ния r = 20%	Проект А			Проект B			Проект C
годы	Коэффициент дисконтирова- ния r = 20%	Д.П.	PV	Кум.PV	Д.П.	PV	Кум.PV	Д.П.	PV	Кум.PV
0	1,000	-3000	-3000	—	-3000	-3000	—	-3000	-3000	—
1	0,833	0	0	0	0	0	0	1000	833	833
2	0,694	2000	1388	1388	1000	694	694	1000	694	1527
3	0,579	1000	579	1967	2000	1158	1852	1000	579	2106
4	0,482	1000	482	2449	2000	964	2816	2000	964	3070
5	0,402	1000	402	2851	2000	804	3620	2000	804	3874
ЧПС			-149			+620			+874
период окупаемости		3 года		ПО > 5	3 года		4,35 года			3,98 года

Выводы из рассмотренного примера следующие:

Дисконтированная окупаемость служит лучшим критерием, чем недисконтированная (традиционная). Она учитывает, что гривна в начале периода окупаемости дороже, чем гривна в конце периода окупаемости;
Учитывает динамику денежных потоков до периода окупаемости, хотя все же не учитывает потоки денежных средств, возникающих за пределами периода окупаемости;
Величина дисконтированной окупаемости получается больше, чем период окупаемости, рассчитанный традиционным методом;
Критерий период окупаемости очень важен, но не совсем надежный.

Рентабельность инвестиции

В разделе 12.2 было показано как рассчитывается бухгалтерская норма прибыли (рентабельности). Для вычисления бухгалтерской нормы прибыли необходимо разделить среднюю прогнозируемую прибыль от проекта с учетом амортизации, и налогов на среднюю балансовую стоимость инвестиции или на начальную величину инвестиции.

Бухгалтерская рентабельность, как критерий для оценки и выбора проектов обладает рядом серьезных недостатков.

Во-первых. Поскольку этот критерий отражает только среднюю прибыль в расчете на балансовую стоимость инвестиции, то не учитывает тот факт, что немедленные поступления имеют большую стоимость, чем отдаленные во времени. Если в правиле окупаемости не принимается во внимание «при дисконтировании» более удаленные во времени денежные потоки, то в правиле рентабельности в расчете на балансовую стоимость активов им придается слишком большое значение.

Во-вторых. Показатель средней прибыли на балансовую стоимость инвестиции опирается на бухгалтерскую прибыль, а не создаваемые проектом денежные потоки, которые могут сильно различается. Например в таблице 12.4 приведены данные о трех проектах А, В, С.

Табл. 12.4 Данные о денежных потоков и прибыли при I = 9000

Проект		Потоки денежных средств
Проект		год 1	год 2	год 3
А	Поток денежных средств	4000	5000	6000
А	Чистая прибыль	1000	2000	3000
В	Поток денежных средств	5000	5000	5000
В	Чистая прибыль	2000	2000	2000
С	Поток денежных средств	6000	5000	4000
С	Чистая прибыль	3000	2000	1000

У этих проектов среднегодовая прибыль равна 2000 и норма прибыли на среднюю балансовую стоимость инвестиций равна

2000 : (9 × 05) ×100 = 44,4%.

В таблице 12.5 приведены результаты расчета индекса доходности и рентабельности инвестиций тех же проектов. Как видно из сравнения результатов двух таблиц, они имеют существенные различия. Во втором случае расчеты оперируются исключительно потоками денежных средств, порождаемые проектом.

Учетом стоимости денег во времени.

Таблица 12.5

Расчет ЧПС, индекса доходности (ИД) и рентабельности (ROI) при r=20%

годы	Коэф. дисконтирования	Проект А		Проект В		Проект С
годы	Коэф. дисконтирования	ДП	PV	ДП	PV	ДП	PV
1	0,833	4000	3332	5000	4105	6000	4998
2	0,694	5000	3470	5000	3470	5000	3470
3	0,579	6000	3474	5000	2895	4000	2316
 PV			10276		10530		10784
I			9000		9000		9000
ЧПС			1276		1530		1784
ИД			1,14		1,17		1,198
ROI			14,10%		17%		19,80%

В-третьих. Возмещение капитальных затрат происходит согласно произвольно выбранной бухгалтерской схеме начисления амортизация. Поэтому средняя прибыль в расчетах на балансовую стоимость инвестиции зависит от того какие ставки расходов бухгалтер относит на организационные затраты, а какие на капитальные затраты и как они амортизируются.

В-четвертых. Правило окупаемости не совсем надежный критерий. Правило средней прибыли в расчете на среднюю балансовую стоимость инвестиции может быть еще и хуже. Он учитывает альтернативную стоимость денег и не опирается на потоки денежных средств проекта и инвестиционные решения, принятые согласно этому правилу могут быть связаны с рентабельности уже действующей фирмой бизнеса.

Однако, применение коэффициента рентабельности инвестиций (ROI) может привести к неправильным решениям (ошибкам), когда приходится выбирать между двумя взаимоисключающими инвестиционными проектами.

Рассмотрим два следующих проекта.

Расчет при r=10%

Проект	потоки денежных средств		PV	ROI	ЧПС	ИД
Проект	I	ДП	PV	ROI	ЧПС	ИД
А	-1000	2000	1820	82%	820	1,82
В	-5000	7000	7280	45,60%	2280	1,452

Как показывают данные оба проекта хороши. Но у проекта А ROI больше, чем у проекта В, но зато у проекта В ЧПС больше, чем у проекта А. Здравый смысл предсказывает, что если проекты взаимоисключающие, то надо бы принимать проект В, т.е. с более высокой чистой приведенной стоимостью. Тем не менее, если судить по коэффициенту рентабельности, приоритет принадлежит проекту А.

В таких случаях можем решить проблему, рассмотрев коэффициент рентабельности природных инвестиций.

проект	I	ДП	PV	ROI	ЧПС	ИД
В-А	4000	5000	4550	13,75%	550	1,137

Индекс доходности больше единицы и коэффициент рентабельности (ROI) больше нуля, значит лучшим является проект В .

Коэффициент рентабельности инвестиций (ROI) и индекс доходности схожи с принципом чистой приведенной стоимости:

Если ЧПС >0 , то ИД > 1 и ROI >0
Если ЧПС =0 , то ИД = 1 и ROI =0

Общая характеристика показателей.

Показатели, используемые в инвестиционном анализе, предназначенны для оказания помощи лицам принимающим решения в определении того, что рассматриваемый проект соответствует ли требованиям, проявляемый принятым для данной сферы деятельности, рекомендуемой рентабельности, и обеспечивает ли он создание стоимости бизнеса.
Если рассматриваемые проекты независимы друг от друга, то такие показатели, как чистая приведенная стоимость(ЧПС), индекс доходности (ИД), внутренняя норма доходности (ВНД), дисконтированный период окупаемости (ПО) и рентабельность инвестиции(ROI) по отдельности или все вместе адекватно выражать относительную экономическую привлекательность проекта и поможет выступить соответствующий им рейтинг. При этом надо помнить, что критерии чистой приведенной стоимости все же является наиболее важным.
Рассмотренные выше показатели являются финансовыми. Но для принятия инвестиционных решений существенными могут оказаться и не финансовые факторы , которые не отражаются в этих показателях.
Чрезмерное доверие финансовым критериям оценки капиталовложений может искажать смысл стратегической направленности деятельности фирмы. В частности, подобные критерии не редко ориентированы на внутреннее состояние фирмы, тогда как стратегическое планирование требует более широкого взгляда. Особенно стремлением к скорейшему достижению результата может сдерживать инновационный процесс. В частности, возможно, что реализация какого-то проекта прокладывает путь дальнейшему развитию, но финансовый анализ с помощью рассматриваемых показателей врядли отобразит это.
Ни один из перечисленных критериев не учитывает то, каким образом проект будет финансироваться. Поскольку стоимость большинства инвестиционных проектов значительна, то при оценке их финансовой платежеспособности вопрос финансирования должен быть основным.

studfiles.net

Как анализировать внутреннюю норму доходности (IRR)? | статьи

Каждый раз, когда вы предлагаете капитальные затраты, вы можете быть уверены, что старшие руководители захотят выяснить их рентабельность (ROI).

Существует множество методов, которые вы можете использовать для расчета ROI — чистая приведенная стоимость, период окупаемости, индекс прибыльности и внутренняя норма доходности или IRR.

Разберемся, как работает IRR и в каких случаях его лучше использовать.

Что такое внутренняя норма доходности?

IRR — это ставка, при которой проект достигает уровня безубыточности (т.е. окупает себя).

Обычно этот показатель используется финансовыми аналитиками в сочетании с чистой приведенной стоимостью или NPV. Это связано с тем, что оба метода похожи, но используют разные переменные.

С помощью NPV вы определяете ставку дисконтирования для своей компании, а затем вычисляете текущую стоимость инвестиций с учетом этой ставки (здесь подробнее о NPV).

Но для IRR вы рассчитываете фактический доход по денежными потоками проекта, а затем сравниваете его с барьерной ставкой вашей компании (т.е. с минимальным ожидаемым уровнем доходности вашей компании). Если IRR выше, то инвестиции выгодны.

Как рассчитывается IRR?

Это не простой расчет. Например, предположим, что вы предлагаете инвестиции в размере 3 000 д.e., которые принесут 1 300 д.e. за каждый год из следующих 3 лет. Вы не можете просто использовать общий денежный поток в размере 3 900 д.е (1 300 * 3) для определения нормы доходности, поскольку он распространяется на период, превышающий эти 3 года.

Вместо этого вам придется использовать итеративный процесс, в котором вы будете пытаться использовать разные барьерные ставки (или годовые процентные ставки), пока ваш NPV не будет равен нулю.

Для расчета этого показателя вам необязательно углубляться в математику, — вы можете легко вычислить его в Exсel (функция ВСД или IRR) или на финансовом калькуляторе.

Как компании используют его?

Компании обычно используют как NPV, так и IRR для оценки инвестиций.

NPV говорит вам больше об ожидаемой рентабельности, но при этом финансовые аналитики «часто полагаются на IRR в презентациях для нефинансовых людей».

Это связано с тем, что IRR гораздо более прост и интуитивно понятен.

Когда вы говорите: «Если у меня есть проект, где IRR составляет 14%, а наша корпоративная барьерная ставка составляет 10%», ваша аудитория думает: «О, я понимаю. Мы получаем на 4% больше прибыли от этого проекта».

Если бы вы сказали, что NPV в этом проекте составляет 2 млн. д.е., ваша аудитория весьма вероятно попросит напомнить о том, что такое NPV, и может запутаться, прежде чем вы хотя бы частично объясните значение того, что «текущая стоимость будущих денежных потоков от этих инвестиций с использованием нашей 10% барьерной ставки превышает наши первоначальные инвестиции на 2 миллиона д.е.».

Недостатком этого показателя является то, что IRR гораздо более концептуальна, чем NPV. Используя NPV, вы оцениваете денежный доход компании: если предположить, что все предположения верны, этот проект принесет 2 млн. д.е. IRR не дает вам реальных денежных цифр.

Точно так же IRR не затрагивает вопросы масштаба. Например, IRR 20% не говорит вам ничего о сумме денег, которую вы получите. Это 20% от 1 миллиона д.е.? Или от 1 д.е.? Не обязательно быть математиком, чтобы понять, что между этими цифрами есть большая разница.

Какие ошибки делают люди при использовании IRR?

Самая большая ошибка заключается в том, чтобы использовать исключительно IRR.

Гораздо лучше анализировать проект, используя хотя бы один из других методов — NPV и/или срок окупаемости.

Использование только этого показателя может привести к тому, что вы будете принимать плохие решения о том, куда инвестировать с трудом заработанные деньги вашей компании, особенно при сравнении проектов, имеющих разные сроки.

Скажем, у вас есть годичный проект с IRR 20% и 10-летний проект с IRR 13%. Если вы основываете свое решение только на IRR, вы можете поддержать 20%-ный проект IRR. Но это было бы ошибкой. Вам выгоднее IRR 13% в течение 10 лет, чем 20% в течение одного года, если ваша корпоративная барьерная ставка будет составлять 10% в течение этого периода.

Вы также должны быть осторожны с тем, как IRR учитывает временную стоимость денег. IRR предполагает, что будущие денежные потоки от проекта реинвестируются в IRR, а не в стоимость капитала компании, и поэтому этот показатель не так точно отражает связь с капиталом и временной стоимостью денег, как NPV.

Модифицированная внутренняя норма доходности (MIRR), предполагающая, что положительные денежные потоки реинвестируются в капитал фирмы, более точно отражает стоимость и рентабельность проекта.

Тем не менее, следует всегда использовать IRR в сочетании с NPV, чтобы получить более полную картину того, какую отдачу принесут ваши инвестиции.

fin-accounting.ru

Внутренняя норма доходности (IRR) | SPRINTinvest.RU

Внутренняя норма доходности традиционно являет собой второй по значимости критерий принятия инвестиционных решений, который вполне может посоперничать с чистой приведенной стоимостью за право считаться наиболее популярным методом отбора или отсеивания «неблагонадежных» инвестиционных проектов.

Финансовые учебники весьма благосклонно оценивают данный показатель, рекомендуя его к широкому употреблению.

Задача сегодняшней публикации – с рентгеновской беспристрастностью расщепить на составляющие понятие внутренней нормы доходности и предоставить заинтересованному читателю непредвзятый обзор преимуществ и недостатков данного метода, прежде всего, с точки зрения его практического применения.

Норма доходности: предварительные сведения

По традиции освежим в памяти некоторые важные правила, вытекающие из теории чистой приведенной стоимости.

В частности, одно из таких правил указывает на необходимость реализации инвестиционных возможностей, предлагающих большую доходность, нежели размер наличествующих альтернативных издержек.

Сей тезис можно было бы признать абсолютно верным, если бы не многочисленные ошибки, связанные с его истолкованием.

Сталкиваясь с краткосрочными инвестициями, трудностей с трактовкой данного утверждения и выбором альтернатив, как правило, не возникает.

Сложности появляются, когда мы захотим «натянуть» это правило на долгосрочные инвестиции.

Почему так происходит, сейчас мы и разберем.

Расчет истинной доходности инвестиций, приносящих денежный поток единожды в течение года, прост, если не сказать примитивен:

где D – искомая доходность,
C₁ – валовая отдача от инвестиций,
C₀ – размер начальных инвестиций.

Другой способ нахождения того же показателя предполагает «плясать» от чистой приведенной стоимости. Достаточно записать формулу нахождения чистой приведенной стоимости и попытаться найти значение ставки дисконтирования, при которой значение NPV окажется равным нулю:

Решая это простейшее уравнение, находим r:

Фактически оба наших выражения воплощают единую идею.

Коэффициент r знаменует собой норму доходности, то есть ставку дисконтирования, соответствующей нулевому значению чистой приведенной стоимости.

На знак «минус» перед дробью в правой части формулы особого внимания не обращаем; его наличие объясняется отрицательным значением C₀, используемым в формуле расчета ЧПС.

Что такое внутренняя норма доходности

Когда заходит речь о нахождении истинной доходности долгосрочных инвестиций, многие инвесторы и финансовые менеджеры приходят в смятение, которое легко объяснимо.

Увы, простого и удобного инструмента, который позволял бы вручную, на коленках, без излишних умственных затрат рассчитывать искомое значение, до сих пор не придумано…

Для решения этой задачи используется специальный коэффициент, именуемый внутренней нормой доходности, который по сложившейся традиции обозначается как IRR.

Для вычисления этого показателя нужно решить «простейшее» уравнение:

Для случаев, когда T равно 1, 2 и даже 3, уравнение худо-бедно решаемо, и можно вывести относительно простые выражения, позволяющие рассчитать значение IRR посредством подстановки соответствующих данных.

Для случаев, когда T > 3, такие упрощения уже не проходят и на практике приходится прибегать к специальным вычислительным программам либо подстановкам.

Пример расчета внутренней нормы доходности

Теорию легче всего усваивать на конкретных примерах.

Представим, что размер наших первоначальных инвестиций составляет 1500 долл.

Денежный поток по истечении 1-го года будет равен 700 долл., 2-го года – 1400 долл., 3-го года – 2100 долл.

Подставив весь этот набор значений в нашу последнюю формулу, придадим уравнению следующий вид:

NPV = -1500 долл. + 700 долл. / (1 + IRR) + 1400 долл. / (1 + IRR)² + 2100 долл. / (1 + IRR)³ = 0.

Для начала рассчитаем значение NPV при IRR = 0:

NPV = -1500 долл. + 700 долл. / (1 + 0) + 1400 долл. / (1 + 0)² + 2100 долл. / (1 + 0)³ = +2700 долл.

Поскольку мы получили ПОЛОЖИТЕЛЬНОЕ значение NPV, искомая внутренняя норма доходности тоже должна быть БОЛЬШЕ нуля.

Рассчитаем теперь значение NPV, скажем, при IRR = 80 % (0,80):

NPV = -1500 долл. + 700 долл. / (1 + 0,8) + 1400 долл. / (1 + 0,8)² + 2100 долл. / (1 + 0,8)³ = -318,93 долл.

На этот раз мы получили ОТРИЦАТЕЛЬНОЕ значение. Это значит, что и внутренняя норма доходности должна быть МЕНЬШЕ 80 %.

Ради экономии времени мы самостоятельно рассчитали NPV при исходных данных для значений IRR, варьирующихся в пределах от 0 до 100, после чего построили следующий график:

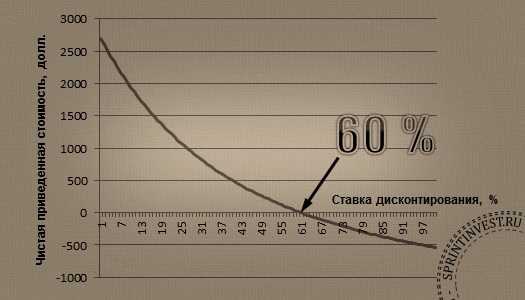
Как следует из графика, при значении IRR, приблизительно равном 60%, NPV будет равняться нулю (то есть пересекать ось абсцисс).

Попытки разыскать в недрах теории внутренней нормы доходности некий инвестиционный смысл приведут нас к следующим умозаключениям.

Если альтернативные издержки МЕНЬШЕ внутренней нормы доходности, инвестиции будут оправданными, и соответствующий проект следует ПРИНЯТЬ.

В противном случае от инвестиций следует ОТКАЗАТЬСЯ.

Обозрим наш график еще раз, чтобы понять, почему это действительно так.

Если значения ставки дисконтирования (размера альтернативных издержек) будут колебаться в пределах от 0 до 60, то есть быть МЕНЬШЕ внутренней нормы доходности, совокупность значений чистой приведенной стоимости будет ПОЛОЖИТЕЛЬНОЙ.

При равнозначности значений альтернативных издержек и внутренней нормы доходности, значение NPV окажется равным 0.

И, наконец, если величина альтернативных издержек ПРЕВЫСИТ размер внутренней нормы доходности, значение NPV будет ОТРИЦАТЕЛЬНЫМ.

Приведенные рассуждения верны для всех случаев, когда, как в нашем примере, график чистой приведенной стоимости имеет равномерно нисходящий вид.

На практике же возможны другие ситуации, разбор которых покажет нам, почему в конечном итоге использование метода внутренней нормы доходности, при прочих равных, может привести к ошибочным выводам в плане обоснованности инвестиционных решений.

Однако это уже тема наших последующих публикаций…

sprintinvest.ru

Внутренняя норма рентабельности — (доход, внутренний коэффициент окупаемости, Internal Rate of Return — IRR) — норма доходности , порожденная инвестициями .

Это та норма доходности ( ставка дисконтирования), при которой незапятнанная данная стоимость инвестиций равна нулю, либо это та ставка дисконта, при которой, как многие выражаются, дисконтированные прибыли от проекта приравниваются инвестиционным растратам.

Внутренняя норма рентабельности определяет максимальную приемлемую ставку дисконта, при которой разрешается инвестировать средства без всяких потерь для собственника данных средств.

IRR = r, при котором NPV = f(r) = 0,

Это значение можно найти из следующего уравнения:

CFt — приток денежных средств в период t;
It — совокупность инвестиций (затрат) в t-ом периоде;
n — совокупное число периодов ( интервалов) t = 0, 1, 2, …, n.

Экономический смысл показателя заключается в том, что он как бы указывает норму доходности, которая ожидается (прибыльность инвестиций) либо очень допустимый уровень инвестиционных издержек в оцениваемый проект. IRR должен быть больше, как мы привыкли говорить, средневзвешенной стоимости инвестиционных ресурсов:

IRR > CC.

Если это условие соблюдается, то инвестор может принять проект, в ином случае он должен будет отклонен.

Плюсы показателя внутренней нормы доходности (IRR) состоят в том, что не считая определения уровня прибыльности инвестиций, также можно сопоставить проекты различного масштаба и как бы различного рода продолжительности.

Данный показатель эффективности инвестиций: внутренняя норма доходности (IRR) имеет главные недочеты:

Во-первых, предполагается что доходный остаток будет реинвестироваться по ставке, равной внутренней норме доходности

Во-вторых, нет своего рода возможности понять , сколько могут принести деньги от инвестиций в абсолютном значении (рубли, доллары).

Внутренняя норма прибыльности может также использоваться

для экономической оценки проектных решений, если известны наиболее приемлемые значения для ВНР ( которые зависят от области их применения) у проектов такого типа;
для оценки степени стойкости инвестиционных проектов по разности ВНР — Е;

investr-pro.ru

Внутренняя норма доходности

Показатель внутренней нормы доходности широко используется при анализе эффективности инвестиционных проектов.

Реализация любого инвестиционного проекта требует привлечения финансовых ресурсов, за которые всегда необходимо платить. Так, за заемные средства платят проценты за привлеченный акционерный капитал — дивиденды и так далее, т.е. предприятие несет некоторые обоснованные расходы на поддержание своего экономического потенциала.

Показатель, характеризующий относительный уровень этих расходов, можно назвать «ценой» авансированного капитала (СС).

При финансировании проекта из разных источников этот показатель определяется по формуле средней арифметической взвешенной. Чтобы обеспечить доход от инвестиционных средств или их окупаемость, необходимо добиться такого положения, когда чистая текущая стоимость будет равна нулю.

Для этого необходимо подобрать такую процентную ставку для дисконтирования членов потока платежей, использование которой обеспечит равенство текущей стоимости ожидаемых денежных оттоков и притоков.

Отсюда IRR (ВНД) – это ставка дисконтирования, при которой NPV = 0.

Такая ставка (барьерный коэффициент) должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке с учетом фактора риска.

Например, если для реализации проекта получена банковская ссуда, то значение IRR показывает верхнюю допустимую границу банковской процентной ставки, превышение которой делает проект убыточным.

Таким образом, смысл этого показателя заключается в том, что инвестор должен сравнить полученные для проекта значения IRR с «ценой» привлеченных финансовых ресурсов (СС).

Если IRR > CC, проект следует принять.

Если IRR = CC – проект ни прибыльный, ни убыточный.

Если IRR < CC – проект следует отвергнуть.

Практически применение данного метода сводится к последовательной итерации, с помощью которой находится дисконтирующий множитель, при котором NPV = 0. Для этого используют формулу

IRR 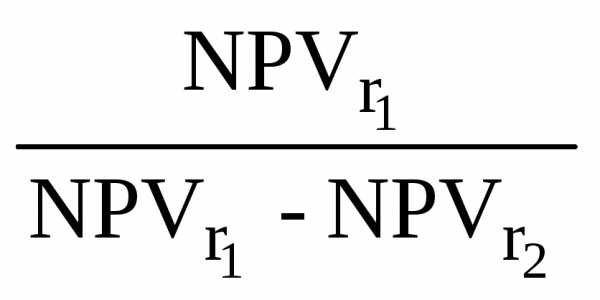= r₁+ · (r₂ – r1),

где r₁% – нижняя ставка дисконтирования; r₂ % – верхняя ставка дисконтирования.

Для расчета IRR выбираются два значения коэффициента дисконтирования r₁ < r₂, таким образом, чтобы в интервале r₁– r₂ , NPV = f(r) меняла свое значение с «+» на «-» или наоборот.

Точность вычислений обратна длине интервала (r₁-r₂) . Наименьшая погрешность достигается при длине интервала 1%.

Смысловое значение IRR включает:

1. При вычислении IRR предполагается полная капитализация получаемых чистых доходов, т.е. все образующиеся свободные денежные средства должны быть либо реинвестированы, либо направлены на погашение внешней задолженности.

2. IRR является граничной ставкой ссудного процента, разделяющей проекты на эффективные и неэффективные, т.е. если нижний гарантированный порог прибыльности инвестиционных затрат превышает среднюю стоимость капитала, то проект может быть рекомендован к осуществлению.

3. IRR определяет максимальную ставку платы за привлекаемые источники финансирования проекта, при которой он остается безубыточным (максимальная ставка по кредитам, наибольший уровень дивидендов и др.).

4. IRR содержит меньший уровень неопределенности, чем NPV, так как все составляющие IRR определяются внутренними данными, (характеризующими инвестиционный проект) и отсутствием экспертной оценки, вносящей субъективные элементы.

Риск и неопределенность при расчете IRR. Все проекты сопряжены с риском и неопределённостью, поскольку они связаны с будущими событиями, которые являются непредсказуемыми. При учете риска и неопределённости используются два основных метода:

1. Корректировка ставки дисконтирования.

2. Анализ чувствительности.

Первый метод компенсирует риск. Например, если капитальные издержки компании составляют 15 % , то она может увеличить их до 20%, если полагает, что проект сопряжён с риском, превышающим нормальный. И наоборот, она может уменьшить ставку дисконтирования до 10%, если считает, что проект сопряжен с риском меньше нормального.

При этом следует решить:

1. Что подразумевать под «нормальным» риском?

2. Как измерить риск относительно «нормального»?

3. Как вычислить, насколько надо изменить величину капитальных издержек?

Решению этих проблем может помочь применение модели ценообразования капитальных активов (соотношение ожидаемого риска и дохода).

Анализ чувствительности. Лицо принимающее решение заинтересовано в том, насколько чувствительно NPV к изменениям в любой из оценок потоков наличности.

Критический момент наступает, когда NPV упадет до нуля, что повлечет отклонение проекта. В анализе чувствительности каждая оценка исследуется по очереди (постоянные и переменные издержки, выручка от реализации, ставка дисконтирования, спрос и другие), чтобы установить, как она должна измениться, чтобы решение по проекту изменилось на обратное.

Отсюда чувствительность любого отдельно взятого потока наличности может быть рассчитана как отношение чистой дисконтированной стоимости (NPV) к дисконтированной стоимости исследуемого потока наличности.

Ограничения этого метода:

1. Каждый параметр варьируется по очереди, остальные считаются неизмененными.

2. Нет формального анализа риска.

3. Анализ чувствительности не сообщает, какая должна быть реакция на его результаты.

Достоинства показателей IRR.

Преимущества метода:

1. Он информативен.

2. Учитывает временную ценность денег.

3.Точен и реалистичен.

Недостатки показателя IRR:

1. Требует много времени для расчетов.

2. Зависит от объема финансирования.

3. Не учитывает изменение объемов инвестиций по конкурирующим проектам.

studfiles.net

IRR — внутренняя норма доходности

Область применения

Внутренняя норма доходности определяет максимально приемлемую ставку дисконта, при которой можно инвестировать средства без каких-либо потерь для собственника.

Описание

Внутренняя норма доходности IRR (Internal Rate of Return) является широко используемым показателем эффективности инвестиций. Под этим термином понимают ставку дисконтирования, при которой чистая текущая стоимость инвестиционного проекта равна нулю. На практике значение $IRR$ сравнивается с заданной нормой дисконта $r$. При этом, если $IRR> r$, то проект обеспечивает положительную величину $NPV$ и процент дохода, равный $(IRR-r)$.

Внутренняя норма доходности определяется по формуле:

$$NPV = \sum \limits_{i=0}^{n} \frac{CF_i}{(1+IRR)^i} — \sum \limits_{i=0}^{n}\frac{CI_i}{(1+IRR)^i}, \,\mbox {при} \, NPV = 0$$

Величину $IRR$ можно определить ещё одним способом. Для этого сначала рассчитывают $NPV$ при различных уровнях дисконтной ставки $r$ до того значения, пока величина $NPV$ не станет отрицательной. После этого значение $IRR$ находят по формуле:

$IRR=r_a+(r_b — r_a)\frac{NPV_a}{NPV_a — NPV_b}$,

должно соблюдаться неравенство $NPV \_a > 0 > NPV \_b \, \mbox {и}\,\ r\_b > IRR > r\_a$.

Достоинством показателя $IRR$ является то, что он дает возможность сравнить проекты разного масштаба и различной длительности. Например, эффективность проекта с $IRR$, равной 30%, достаточна в случае, если для его реализации необходимо использовать кредит в банке стоимостью 10% годовых.

Недостатки показателя внутренней нормы доходности:

По умолчанию предполагается, что положительные денежные потоки реинвестируются по ставке, равной внутренней норме доходности. Когда $IRR$, особенно привлекательного инвестиционного проекта равен, к примеру, 80%, то имеется в виду, что все денежные поступления должны реинвестироваться при ставке 80 %. Однако маловероятно, что предприятие обладает ежегодными инвестиционными возможностями, которые обеспечивают рентабельность в 80%. В данной ситуации показатель внутренней нормы доходности ($IRR$) завышает эффект от инвестиций. В случае, если $IRR$ близко к уровню реинвестиций фирмы, то этой проблемы не возникает.
Нет возможности определить, сколько принесет денег инвестиция в абсолютных значениях (рублях, долларах).
При произвольном чередовании притоков и оттоков денежных средств в случае одного проекта могут существовать несколько значений $IRR$. Поэтому принимать однозначное решение на основе показателя $IRR$ нельзя.

Если имеется несколько альтернативных проектов с одинаковыми значениями $NPV$, $IRR$, то при выборе окончательного варианта инвестирования учитывается длительность инвестиций – дюрация. Дюрация (D) – это средневзвешенный срок жизненного цикла инвестиционного проекта или его эффективное время действия. Она позволяет привести к единому стандарту самые разнообразные по своим характеристикам проекты (по срокам, количеству платежей в периоде, методам расчета причитающегося процента). Этот метод основан на расчете момента, когда проект будет приносить доход и сколько поступлений дохода будет каждый месяц, квартал или год на протяжении всего срока его действия. В результате менеджеры получают сведения о том, как долго окупаются инвестиции доходами, приведенными к текущей дате. Для расчета дюрации используют следующую формулу:

$D=\frac{\sum \limits_{i=1}^{n} i*PV_i}{\sum \limits_{i=1}^{n}PV_i}$,

где $PV_i=\frac{CF_i}{(1+r)^i}$ — текущая стоимость доходов за i периодов до окончания срока действия проекта,

$i$ — периоды поступления доходов.

Алгоритм

Определение индекса рентабельности: PI.
Рассчитываем дюрацию D.
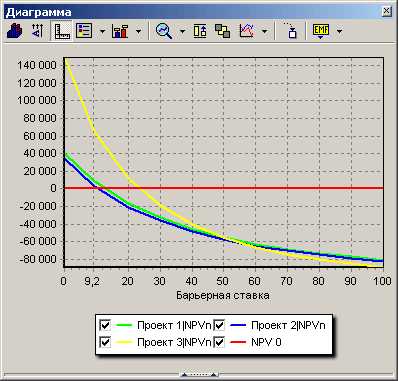
Используем метод последовательного приближения для расчета внутренней нормы доходности. Подбираем барьерные ставки так, чтобы найти минимальные значения NPV по модулю, и затем проводим аппроксимацию:
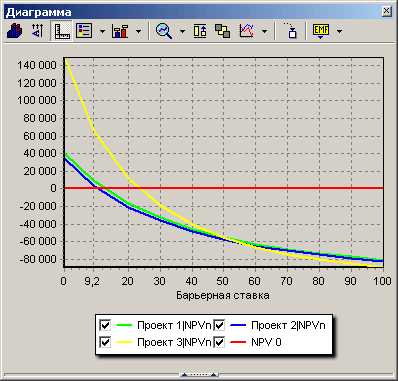
- строим график NPV;
- определяем значения барьерных ставок для трёх проектов. Например, Rate1_min = 10, Rate1_max = 20. Так как мы предполагаем, что на рассматриваемом участке функция NPV(r) близка к прямолинейной, то для увеличения точности расчета IRR необходимо приближать значения барьерных ставок к точке, в которой NPV=0;
- вносим значения барьерных ставок в переменные проекта;
- рассчитываем значение IRR.

Требования к данным

Имя поля	Метка поля	Тип данных	Вид данных
Year	Год	Целый	Непрерывный
Cash_flow	Денежные поступления	Вещественный	Непрерывный
Rate	Норма дисконта	Вещественный	Непрерывный
Investment	Инвестиции	Вещественный	Непрерывный
Project	Проект	Строковый	Дискретный

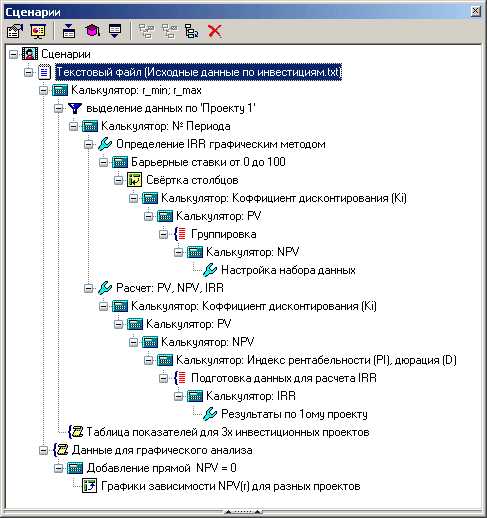
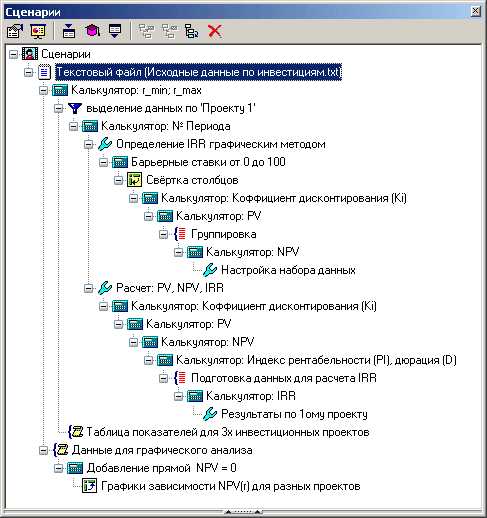
Сценарий

basegroup.ru

Внутренняя норма рентабельности – Внутренняя норма рентабельности (IRR): формула расчета показателя