Всё про доходность инвестиций: как рассчитать, формулы

Для того, чтобы выбрать среди огромного количества вариантов инвестиций в Интернете самые перспективные, инвесторам нужны универсальные критерии оценки. Самый очевидный — это доходность, мера увеличения или уменьшения суммы инвестиций за определенное время.
Доходность измеряется в процентах и показывает отношение прибыли от реальных или финансовых инвестиций к количеству вложенных денег. Она показывает не сколько конкретно инвестор заработал, а эффективность вложений. Инвесторы при анализе вариантов инвестиций смотрят на доходность в первую очередь, нередко забывая о возможных инвестиционных рисках.
Я бы не писал большую статью, если бы для всех случаев работала одна формула — подводных камней при расчёте доходности в разных случаях хватает. В принципе, можно не заморачиваться и использовать для этих целей мой бесплатный инструмент, но все же желательно разобраться в сути вопроса.
В статье рассказывается о часто встречающихся ситуациях, связанных с доходностью инвестиций. Будет много математики класса эдак 8-го, так что готовьтесь 😉 Приятного прочтения! Содержание:
Что такое доходность? Формулы расчёта доходности инвестиций
Базовая формула доходности инвестиций выглядит так:
Сумма вложений — это первоначальная сумма инвестиций плюс дополнительные вложения («доливки»). Инвестиционная прибыль может состоять из разницы между ценой покупки и продажи актива или чистой прибыли инвестиционного проекта. Также сюда могут быть включены регулярные выплаты по источникам пассивного дохода (например, дивиденды акций).
Если неизвестна прибыль, но вы знаете начальную сумму вложений и текущий баланс (суммы покупки и продажи актива тоже подойдут) — пользуйтесь такой формулой:
Доходность инвестиций измеряется в процентах и может служить надежным ориентиром для сравнения двух инвестиционных проектов. Очень показательным выглядит такой пример:
Проект А — 1000$ прибыли за год при начальных инвестициях 5000$. Доходность — 1000$/5000$ = 20%
Проект Б — 1000$ прибыли за год при начальных инвестициях 2000$. Доходность — 1000$/2000$ = 50%
Очевидно, проект Б выгоднее, так как дает более высокую отдачу на вложения, несмотря на то, что чистая прибыль инвестора одна и та же — 1000$. Если увеличить сумму инвестиций в проект Б до 5000$, при доходности 50% за год инвестор заработает уже 2500$.
То есть доходность четко показывает, в каком проекте при прочих равных инвестор заработает больше. Поэтому инвестор с ограниченным размером инвестиционного портфеля старается подобрать активы с более высокой доходностью.
↑ К СОДЕРЖАНИЮ ↑
Расчёт доходности за несколько периодов инвестирования
На практике часто встречаются ситуации, когда инвестиции работают много периодов подряд — начинают работать простые (прибыль снимается после каждого периода) или сложные проценты (прибыль реинвестируется).
Формулы сложных процентов рассчитаны на то, что ставка доходности всегда остаётся постоянной. Но так бывает, пожалуй, только в банках — намного чаще доходность за каждый новый временной период будет отличаться. Как вычислить доходность инвестиций в таком случае?
Если в конце каждого инвестиционного периода прибыль снимается, то все просто — складываем доходности:
Например, если проект принес 5% в первый год и 10% во второй — то таки да, доходность за 2 года составит 15%. Но только при условии вывода прибыли или покрытия убытков. Чаще инвесторы не заморачиваются этим и реинвестируют полученный доход. Для таких ситуаций формула расчёта доходности меняется — мы теперь не складываем, а перемножаем:
Покажу на примере, чтобы было понятнее:
Инвестиционный проект принес 15% за один год, 10% за второй и 20% за третий. Прибыль реинвестируется (работают сложные проценты). Какова итоговая доходность проекта?
Доходность = ((15% + 1)*(10%+1)*(20%+1) — 1) * 100% = (1.15*1.10*1.20 — 1)*100% = (1.518-1)*100% = 0.518*100% = 51.8%
По предыдущей формуле мы получили бы 15%+10%+20% = 45% доходности. Разница в 6.8% достигнута за счёт реинвестирования прибыли — и если её не учитывать, можно получить весьма неточные показатели доходности.
↑ К СОДЕРЖАНИЮ ↑
Расчёт доходности инвестиций с учётом вводов и выводов
Задачка, которая актуальна больше для активных вебинвесторов — они могут перетасовывать свой инвестиционный портфель даже чаще чем раз в неделю.
Для начала, что такое вводы и выводы? Это любое изменение начального инвестиционного капитала, которое не связано с получением прибыли или убытка. Самый простой пример — ежемесячные пополнения инвестиционного счёта из зарплаты.
Каждый раз при вводе или выводе средств меняется знаменатель нашей формулы доходности — сумма вложений. Чтобы вычислить точную доходность вложений, необходимо узнать средневзвешенный размер вложений, рассчитать прибыль от инвестиций с учётом вводов/выводов и вычислить таким образом доходность. Начнем с прибыли, формула будет такой:
Все операции по инвестиционным счетам обычно записываются в специальном разделе вроде «История платежей» или «История переводов».
Как узнать средневзвешенный размер вложений? Вам нужно разбить весь период инвестирования на части, разделенные операциями ввода и вывода. И воспользоваться формулой:
Ворд не очень хочет слушаться и формула получилась корявой на вид. Объясню её на пальцах — мы считаем «рабочую» сумму вложений в каждый из периодов между операциями ввода и вывода и умножаем её на длину периода (в днях/неделях/месяцах), который эта сумма проработала. После всё складываем и делим на полную длину периода, который вас интересует.
Давайте теперь на примере посмотрим как это работает:
Инвестор вложил 1000$ в инвестиционный инструмент. Через 4 месяца инвестор решил добавить еще 300$. Еще через 6 месяцев инвестору понадобились деньги, он снял 200$. В конце года инвестиционный счёт достиг размера 1500$. Какова доходность инвестиционного инструмента?
Шаг 1 — рассчитываем полученную инвестиционную прибыль:
Прибыль = (1500$ + 200$) — (1000$ + 300$) = 400$
Шаг 2 — считаем средневзвешенный размер вложений:
Сумма вложений = (4*1000$ + 6*(1000$+300$) + 2*(1000$+300$-200$))/12 = (4000$+7800$+2200$)/12 = 1166.67$
Шаг 3 — считаем доходность:
Доходность = (400$/1166.67$) * 100% = 0.3429 * 100% = 34.29%
И никак не 50%, если бы мы проигнорировали вводы и выводы — (1500$-1000$)/1000$ * 100% = 50%.
↑ К СОДЕРЖАНИЮ ↑
Расчёт средней доходности инвестиций
Поскольку доходность многих инвестиционных инструментов постоянно меняется, удобно использовать некоторый усредненный показатель. Средняя доходность позволяет привести колебания доходности к одному небольшому числу, которое удобно использовать для дальнейшего анализа и сравнения с другими вариантами инвестиций.
Есть два способа рассчитать среднюю доходность. Первый — по формуле сложных процентов, где у нас есть сумма первоначальных инвестиций, полученная за это время прибыль, а также мы знаем количество периодов инвестирования:
Начальная сумма инвестиций — 5000$. Доходность за 12 месяцев составила 30% (сразу в уме переводим 5000$*30% = 1500$). Какова средняя месячная доходность проекта?
Подставляем в формулу:
Средняя доходность = (((6500/5000)^1/12) — 1) * 100% = ((1.3^1/12) — 1) * 100% = (1.0221 — 1) * 100% = 0.0221 * 100% = 2.21%
Второй способ ближе к реальности — есть доходности за несколько одинаковых периодов, надо посчитать среднюю. Формула:
Проект в первый квартал принес 10% доходности, во второй 20%, в третий -5%, в четвертый 15%. Узнать среднюю доходность за квартал.
Подставляем:
Средняя доходность = (((10%+1)*(20%+1)*(-5%+1)*(15%+1))^(1/4) — 1) * 100% = ((1.1*1.2*0.95*1.15)^(1/4) — 1) * 100% = (1.0958 — 1) * 100% = 0.0958 * 100% = 9.58%
Один из частных случаев вычисления средней доходности — определение процентов годовых, с которыми мы сталкиваемся на каждом шагу в виде рекламы банковских депозитов. Зная доходность инвестиций за определенный период, мы можем рассчитать годовую доходность по такой формуле:
Инвестор вложил 20000$ и за 5 месяцев (округлим до 150 дней) заработал 2700$ прибыли. Сколько это в процентах годовых? Подставляем:
Доходность = (2700$/20000$ * 365/150) * 100% = (0.135 * 2.4333) * 100% = 0.3285 * 100% = 32.85% годовых
↑ К СОДЕРЖАНИЮ ↑
Взаимосвязь доходности и риска инвестиций
Чем больше доходность — тем лучше, вроде бы очевидно. Это правило хорошо работало бы среди безрисковых активов, но таких просто не существует. Всегда есть вероятность потерять часть или всю сумму инвестиций — такова их природа.
Более высокая доходность намного чаще достигается за счет дополнительного увеличения рисков, чем за счёт более высокого качества самого инструмента. Это подтверждается реальными данными — когда я проводил исследование 3000 ПАММ-счетов компании Alpari, обнаружил сильную взаимосвязь между показателем риска СКО (среднеквадратическое отклонение) и доходностью за год:
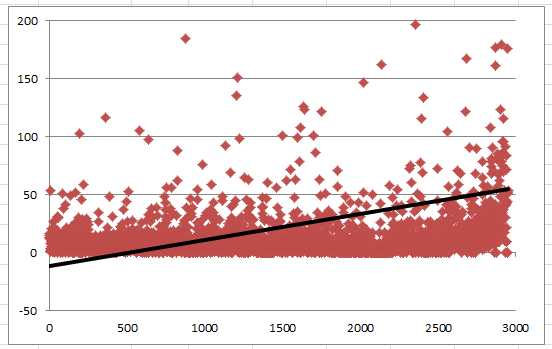
Ось X — доходность за год, ось Y — СКО. Линия тренда показывает, что чем выше годовая доходность, тем выше риски ПАММ-счёта в виде показателя СКО.
Такая взаимосвязь простыми словами — это корреляция, причем достаточно сильная. В исследовании 3000 ПАММ-счетов я рассчитывал корреляцию показателя СКО и доходности и получил значение 0.44, что на такой большой выборке означает крепкую зависимость. Другими словами, взаимосвязь доходности и рисков подтверждается математически.
Задача инвестора — найти собственный баланс между доходностью и риском, точнее определить свою склонность к рискованным вложениям. Для веб-инвестиций минимальная допустимая доходность — на уровне банковской, умноженная на два (большой банк сам по себе надежнее форекс-брокера). Дальше уже зависит от инвестора — сконцентрироваться на минимизации рисков и получать x2-x3 от банковской доходности или пытаться взять на себя дополнительные риски чтобы заработать больше.
Все приведенные выше формулы позволяют рассчитать конечную доходность инвестиций — мы вложили, прошло время, деньги получили. Если говорить о таких инвестиционных инструментах, как ПАММ-счета, торговые роботы, копирование сделок — этого мало, существуют торговые риски и множество других подводных камней, которые могут привести к ненужным потерям.
Инвестор должен знать, что будет происходить с его деньгами в процессе, по этой причине эти инструменты всегда сопровождаются графиками доходности.
↑ К СОДЕРЖАНИЮ ↑
Графики доходности
График доходности — незаменимый инструмент для анализа вариантов инвестирования. Он позволяет посмотреть не просто на общий результат вложений, но и оценить происходящее в промежутке между событиями «вложение денег» и «вывод прибыли».
Существует несколько видов графиков доходности. Чаще всего встречается накопительный график доходности — он показывает, насколько вырос бы в % первоначальный депозит, на основе доходностей за несколько временных промежутков или по результатам отдельных сделок.
Примерно вот так выглядит накопительный график доходности:
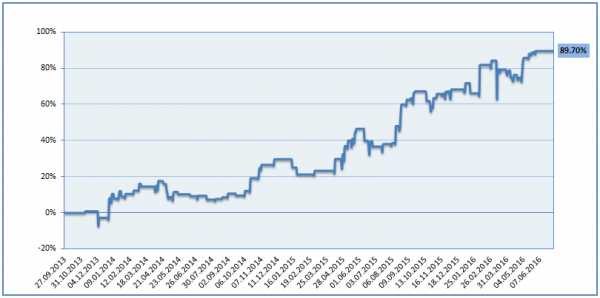
График чистой доходности инвестора ПАММ-счёта Solandr
По нему можно понять несколько важных вещей — например, равномерно ли растёт прибыль (чем более гладкий график, тем лучше), насколько большие просадки (то есть незафиксированные потери в процессе инвестирования) могут ожидать инвестора и т.д.
Очень подробно об анализе графиков доходности я писал в статье о том, как выбрать ПАММ-счёт для инвестирования.
Также часто используются графики доходности по неделям или месяцам:
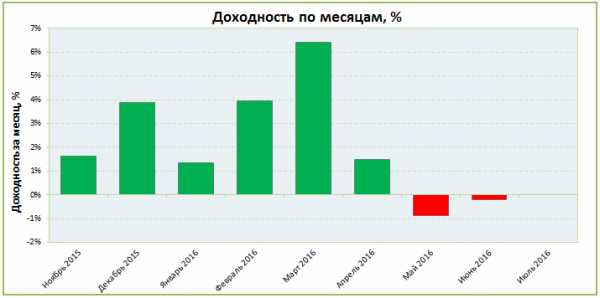
График чистой доходности инвестора ПАММ-счёта Stability Dual Turbo по месяцам
Столбцы говорят сами за себя — март был удачным, а вот за последние три месяца прибыли вообще не было. Если смотреть только на этот график и не брать в расчёт более старые счета Stability, то можно сделать такой вывод — торговая система дала сбой и перестала приносить прибыль. Грамотной стратегией в таком случае будет вывести деньги и ждать пока ситуация вернется в нормальное состояние.
Вообще, графики доходности и ПАММ-счета — это отдельная интересная история.
↑ К СОДЕРЖАНИЮ ↑
Особенности расчёта доходности инвестиций в ПАММ-счета
Начнем с самого очевидного — графики доходности ПАММ-счетов у всех брокеров не соответствуют реальной доходности инвестора! То что мы видим — доходность именно ПАММ-счёта, то есть всей суммы инвестиций, включая и деньги управляющего, и комиссию за управление.
Когда мы видим такие цифры:
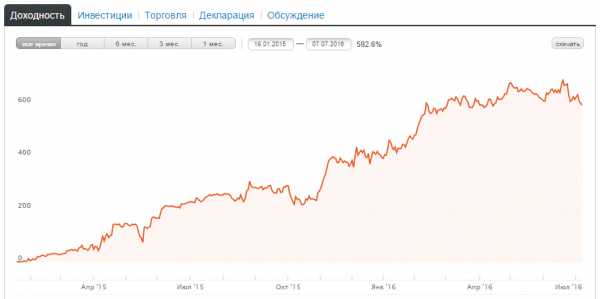
600% за полтора года, рука сразу же тянется к кнопке «Инвестировать», золотая жила же! Однако если мы учтем 29% комиссии управляющего, то реальная доходность окажется такой:
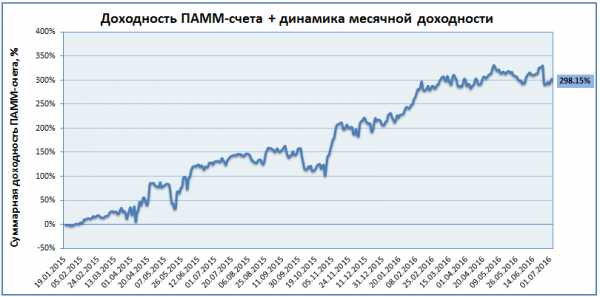
В 2 раза меньше! Я не спорю, 300% за полтора года тоже смотрятся отлично, но это далеко не 600%.
Ну а если углубиться в суть, то доходность ПАММ-счёта считается так:
- Общая доходность считается по формуле доходности за несколько периодов с реинвестированием.
- Положительный результат уменьшается на процент комиссии управляющего, кроме случаев в п.4 и 5.
- Отрицательный результат всегда остается как есть.
- Если положительный результат получен после убытка, он не уменьшается из-за комиссии, пока общая доходность не обновит максимум.
- Если после положительного результата превышен максимум общей доходности — комиссия снимается только с той части, которая превысила максимум.
В итоге получаем весьма замороченную формулу, которая необходима для высокой точности расчётов. Что делать, если вам нужно посчитать чистую доходность инвестора ПАММ-счёта? Предлагаю использовать такой алгоритм:
- Общая доходность считается по формуле доходности за несколько периодов с реинвестированием.
- Положительный результат уменьшается на процент комиссии управляющего.
- Отрицательный результат уменьшается на процент комиссии управляющего.
Все что нужно — умножить официальные цифры доходности ПАММ-счёта на единицу минус комиссия управляющего. Причем не итоговый результат, а данные с графика ПАММ-счёта (в Альпари их можно скачать в удобном виде) и посчитать по формуле доходности за несколько периодов.
Для наглядности посмотрите на один и тот же график доходности, посчитанный тремя способами:
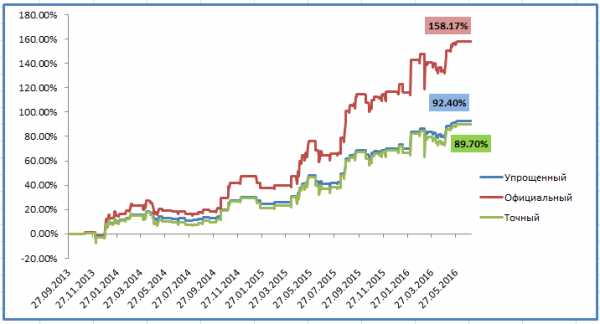
Разница с учётом и без учёта комиссии управляющего — почти в 2 раза! По упрощенному алгоритму мы получили результат 92%, по точному — 89%. Разница не существенная, но для тысяч процентов она станет вполне заметной:
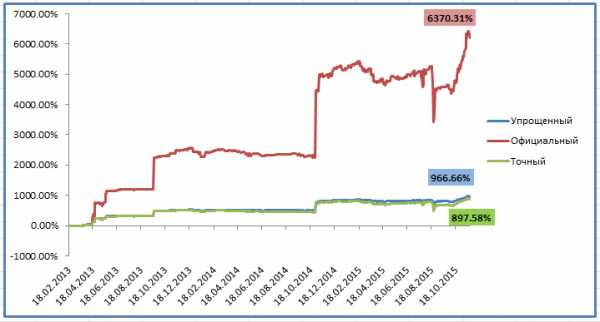
Реальная доходность инвестора ниже в 6 раз, а разница между точным и упрощенным алгоритмом 70% — на больших цифрах всё заметнее.
Кстати, вы хотите знать, откуда вообще берется эта разница? Кроме того, что упрощенный способ подсчета доходности уменьшает размер просадок, есть еще одна фишка — регулярные выплаты вознаграждения управляющего уменьшают вашу долю в ПАММ-счёте.
Вы все поймете, взглянув на эту картинку:
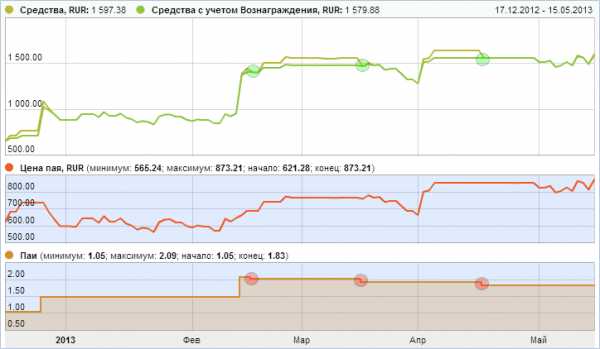
Зелеными кружками показаны моменты выплаты вознаграждения управляющего, красными — уменьшение ваших паёв в ПАММ-счёте. Что такое пай? Это ваша доля в ПАММ-счёте, ваш кусочек общего пирога прибыли.
Для понимания подойдет такое сравнение — паи это определенное количество акций ПАММ-счёта. По этим акциям вы получаете дивиденды — процент от прибыли компании. Количество акций уменьшается — снижаются дивиденды, соответственно и доходность вложений.
Почему же паи уменьшаются? Дело в том, что изначально вы получаете прибыль на всю сумму своих инвестиций — как и должны. Наступает момент выплаты комиссии управляющего — и она берется из вашей суммы, вашего «кусочка пирога». Кусочек стал меньше со всеми вытекающими.
То, что я вам показал — это не плохо, это как есть. Так работают ПАММ-счета, а вкладывать деньги или нет — выбор всегда за вами.
↑ К СОДЕРЖАНИЮ ↑
Друзья, я понимаю что статья довольно сложная, поэтому если есть какие-либо вопросы — задавайте их в комментариях, я постараюсь ответить. И не забывайте делиться статьёй в соцсетях, это лучшая благодарность автору:
Ну и пожелание напоследок: инвестируйте в действительно доходные проекты!
 Автор: Александр Дюбченко (добавляйтесь в друзья Вконтакте и на Facebook). С 2016 года веду блог об инвестировании в Интернете, изучаю инвестиции в ПАММ-счета, акции, криптовалюты, драгоценные металлы, валютный рынок. Также разрабатываю вспомогательные инструменты для инвесторов на основе MS Excel. Всегда готов ответить на любые ваши вопросы.
Автор: Александр Дюбченко (добавляйтесь в друзья Вконтакте и на Facebook). С 2016 года веду блог об инвестировании в Интернете, изучаю инвестиции в ПАММ-счета, акции, криптовалюты, драгоценные металлы, валютный рынок. Также разрабатываю вспомогательные инструменты для инвесторов на основе MS Excel. Всегда готов ответить на любые ваши вопросы.webinvestor.pro
|
Поиск Лекций
Использование критерия NPV теоретически обоснованно, и в целом он считается наиболее корректным измерителем эффективности инвестиций. Вместе с тем применение абсолютных показателей при анализе проектов с различными исходными условиями (первоначальными инвестициями, сроками экономической жизни и др.) может приводить к затруднениям при принятии управленческих решений. Пример 2.3 Предположим, что рассматриваются два проекта. Принятая норма дисконта составляет 10%. Соответствующие оценки денежных потоков и расчет NPV приведены в табл. 2.3. Т а б 1 и ц а 2.3. Условия реализации проектов (пример 2.3)
Чистая современная стоимость обоих проектов составляет 5000 и в случае необходимости выбора не позволяет однозначно определить лучший вариант. Поэтому наряду с абсолютным показателем эффективности инвестиций NPV используются также и относительные — индекс рентабельности и внутренняя норма доходности.
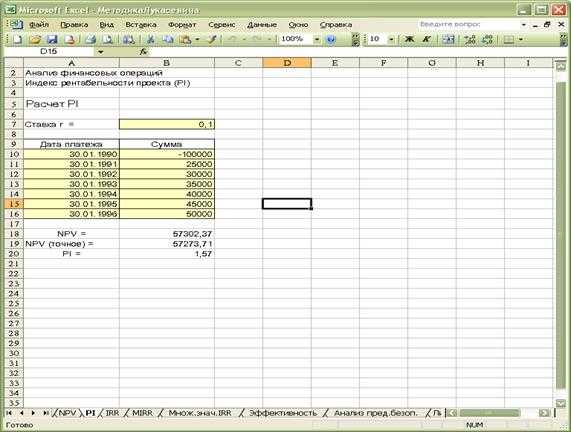
Индекс рентабельности (benefit-cost ratio, profitability index — РГ) показывает, сколько единиц современной величины денежного потока приходится на единицу предполагаемых первоначальных затрат. Для расчета этого показателя используется следующая формула Если величина критерия PI > 1, то современная стоимость денежного потока проекта превышает первоначальные инвестиции, обеспечивая тем самым наличие положительной величины NPV. При этом норма рентабельности превышает заданную, и проект следует принять. При PI = 1 величина NPV = О, и инвестиции не приносят дохода. Если PI<1, проект не обеспечивает заданного уровня рентабельности и его следует отклонить. Общее правило PI: если Р1> 1, то проект принимается, иначе — его следует отклонить. На Листе5 введите данные таблицы 2.3 и рассчитайте индексы рентабельности для примера 2.3 согласно формулам:. Р1Х= 15000/ 10000= 1,50; Ply = 105 000 /100 000 = 1,05. Переименуйте Листе5 в PI. Таким образом, проект X обеспечивает большую рентабельность инвестиций и в случае невозможности реализации обоих проектов ему следует отдать предпочтение. Несмотря на то, что в ППП EXCEL нет специальной функции для вычисления индекса рентабельности, определить его можно довольно легко, например, делением ячейки, содержащей функцию расчета NPV, на ячейку, содержащую величину первоначальных инвестиций, и последующим прибавлением к результату единицы. Рассчитаем индекс рентабельности для примера 2.1. Для этого в ячейке В20 листа NPV сформированной ранее таблицы задайте одну из следующих формул (рис. 2.6): -B18 / В10 + 1 (Результат: 1,57) -B19 / В610 + 1 (Результат: 1,57). Знак минус в формуле необходим для получения положительного результата, так значение ячейки В6 (первоначальные инвестиции) — отрицательная величина. Сохраните полученную таблицу на магнитном диске.
Рис. 2.6. Расчет индекса рентабельности Применение показателя PI часто бывает полезным в случае, когда существует возможность финансирования нескольких проектов, но при этом инвестиционный бюджет фирмы ограничен. Пример 2.4 Фирма рассматривает возможность участия в финансировании шести проектов, предполагаемые условия реализации которых приведены в табл. 2 4. Инвестиционный бюджет фирмы равен 250 000 ден.ед. Перейдите на Лист6 и переименуйте его в Проекты A-F. Создайте шаблон таблицы 2.4. Таблица 2.4. Условия реализации проектов для примера 2.4
Для расчета NPV=PV‑I введите в соответствующие ячейки формулы. Также введите формулы для расчета PI=PV/I в соответствующие ячейки. Результаты сравните с таблицей 2.4.1. Таблица 2.4.1 Условия реализации проектов для примера 2.4
Как видим по данным табл. 2.4.1, все проекты имеют положительную NPV и, если бы инвестиционный бюджет фирмы не был ограничен суммой в 250 000 ден.ед., их следовало бы принять. Однако в силу ограниченности бюджета может быть реализован только тот набор (портфель) проектов, при котором суммарные инвестиции не превышают 250 000 ден.ед. В данном случае существует несколько таких портфелей, поэтому возникает проблема выбора наиболее эффективной комбинации проектов. В условиях ограниченного бюджета наиболее эффективен (оптимален) для фирмы такой портфель проектов, который обеспечивает наибольшую отдачу вложенных средств и в конечном результате генерирует максимальную NPV. Оптимальный портфель инвестиций в подобных условиях можно получить путем последовательного включения проектов в порядке убывания индексов рентабельности и проверки соблюдения ограничений. Расположим проекты, приведенные в табл. 2.4, в порядке убывания индексов рентабельности (выполните сортировку данных по убыванию значений в поле PI). Добавьте столбец и рассчитайте NPV нарастающим итогом. Результаты представлены в таблице 2.5.
Та блица 2.5. Классификация проектов по индексам рентабельности
Как видим по данным из табл. 2.5, оптимальный в этих условиях портфель инвестиций будет состоять из проектов С, D и В. При этом суммарная NPV портфеля равна: NPV =NPV(C) + NPV(D) + NPV(B) = 106 000,00 ден.ед. Более эффективное решение подобных проблем может быть получено при использовании методов математического программирования и рассмотрено ниже. Индекс рентабельности не всегда обеспечивает однозначную оценку эффективности инвестиций, и проект с наиболее высоким PI может • не соответствовать проекту с наиболее высокой NPV. В частности, использование индекса рентабельности может привести к ошибочным результатам при оценке взаимоисключающих проектов. Рассмотрим следующий пример. Пример 2.5 Фирма рассматривает возможность участия в финансировании двух взаимоисключающих проектов, предполагаемые условия реализации которых приведены в табл. 2.6. Принятая норма дисконта для проектов одинакова и равна 10%. Необходимо выбрать наиболее эффективный проект инвестиций. На Листе7 сделайте расчеты как показано в таблице 2.6. Таблица 2.6. Потоки платежей проектов (пример 2.5)
Определим индексы рентабельности для проектов 1 и 2: PI1 = 388,43 / 100,00 = 3,88; Р12 = 34 927,52 / 10 000,00 = 3,43. Нетрудно заметить, что при наличии у фирмы соответствующих средств второй проект предпочтительнее, так как он генерирует большую NPV. Однако индекс рентабельности «отдает» предпочтение первому проекту. Обычно расчет индекса рентабельности дополняет расчет NPV с целью отбора проектов, порождающих максимальную современную стоимость на единицу затрат.
Рекомендуемые страницы: Поиск по сайту |
|
poisk-ru.ru
Индекс рентабельности инвестиционного проекта :: BusinessMan.ru
Когда речь заходит об инвестициях, неизменно возникает вопрос об их целесообразности. Сделать оценку финансирования проекта поможет индекс рентабельности. Он делает возможным подсчитать, каково же будет соотношение доходов и расходов инвестора в плановом периоде. При помощи индекса рентабельности выражается в цифрах то, сколько прибыли принесет каждая денежная единица вложений своему владельцу.
Рентабельность проекта
При помощи индекса рентабельности проекта производится оценка его прибыльности. Эти расчеты применимы к любому уровню и виду экономической деятельности.
Индекс рентабельности проекта позволяет определить уровень доходности проекта. Если же таковых несколько, этот показатель сделает возможным выбрать такой, при котором минимальные затраты приведут к максимально возможной прибыли инвестора.
Рассматриваемый показатель универсален, т. е. позволяет оценить рентабельность проекта как на микро-, так и на макроуровне. Масштабы для него не имеют значения. Также рассматриваемый показатель еще называют индексом рентабельности вложенного капитала.
От точности, качества производимых расчетов зависит возможность сделать адекватные выводы об инвестировании. За проведение сбора данных и их анализ ответственны финансовые менеджеры.
Индекс рентабельности
Что он собой представляет? Индекс рентабельности (от англ. Profitability Index, PI) является одним из инструментов финансового анализа при оценке реализации инвестиционной деятельности. Он связан с другим немаловажным понятием.
Сущностью расчета индекса рентабельности является модификация такого показателя, как NPV (Net Present Value) — дисконтированная приведенная стоимость.
Разница этих двух показателей заключается в возможности PI (индекса рентабельности) учитывать первоначальные инвестиции. NPV дает оценку только будущему дисконтированному (чистому) денежному потоку.
Такая ситуация говорит о преимуществе PI, если требуется из нескольких возможных вариантов выбрать один. Ранжировать имеющиеся пути инвестирования при помощи формулы индекса рентабельности выгодно при ограниченности финансовых ресурсов.
Расчет индекса
Индекс рентабельности, формула которого представлена ниже, позволяет получить величину соотношения ожидаемой стоимости вложений инвестора.
PI = NPV/I, где:
- NPV — чистые денежные потоки;
- I — инвестиции.
Инвестиции в этом случае рассматриваются как финансовый показатель и в расчет берутся без минуса.
NPV = CFn/(1+r)n, где:
- CFn — денежный поток в n-периоде;
- r — ставка дисконта;
- n — инвестиционный период.
Иногда расчет индекса рентабельности производится для крупных проектов, в которых инвестиции производятся неодинаково во времени. В этом случае инвестиции дисконтируются по среднегодовой норме отдачи.
Если PI>1, проект рентабельный, его принимают к дальнейшему рассмотрению. Случается PI = 1. Это свидетельствует о необходимости оценить бизнес-план по другим показателям. Такие действия помогут понять, отбросить его или принять.
В случае, когда индекс рентабельности PI меньше 1, проект убыточный и с рассмотрения снимается.
Схема исследования
Исследование по определению доходности инвестирования должно проводиться по определенной схеме.
Первоначально следует определить, какой объем финансовых ресурсов инвестор или предприятие может направить в оборот без ущерба для себя и своей основной деятельности. Следует понимать, что капитал инвестируется с целью увеличить доходы в области именно основной деятельности. Поэтому для расчетов берется во внимание только величина доходов основной деятельности.
Следующий этап предполагает совершить оценку рисков. Чем они выше, тем больший доход должен получить инвестор.
На основе проведенного анализа определяется ставка дисконтирования. После этого индекс рентабельности, формула которого была рассмотрена выше, позволит рассчитать наиболее эффективные способы действий.
Последний этап заключается в расчете величины будущих приведенных денежных потоков, которые поступят в результате инвестиционной деятельности.
Сложности расчетов
Внешняя простота проведения таких расчетов имеет и свои сложности. Одной из них является определение ставки дисконтирования.  Индекс рентабельности определяется в течение определенного периода. За это время на ставку дисконтирования влияет множество факторов, которые порой очень сложно спрогнозировать. Это могут быть самые различные внутренние и внешние политические, экономические и даже природные события.
Индекс рентабельности определяется в течение определенного периода. За это время на ставку дисконтирования влияет множество факторов, которые порой очень сложно спрогнозировать. Это могут быть самые различные внутренние и внешние политические, экономические и даже природные события.
Чем больше жизненный срок проекта, тем сильнее становится фактор неопределенности. Это может привести к ошибочности расчетов при помощи индекса PI.
Также труднопрогнозируемой является оценка размера будущих поступлений от осуществления инвестиционного проекта.
Ставка дисконта
Чтобы расчеты были произведены правильно, необходимо оценить планируемую ставку дисконта. Например, при совершении инвестирования в виде кредитных средств нижней чертой ставки дисконтирования будет ставка процентов по кредиту.
В случае, когда инвестор финансирует проект из персональных средств, то норма доходности этих вложений должна быть выше или равна норме доходности имеющегося у него капитала. Поэтому в рассмотренном случае ставка дисконтирования должна быть меньше ставки налога на прибыль работающего капитала.
Чтобы расчеты были максимально правильными, анализ следует проводить сразу по нескольким показателям.
Ознакомившись с таким понятием, как индекс рентабельности, можно просчитать доходность инвестирования с учетом количества финансируемых средств. Этот показатель поможет также выполнить ранжирование нескольких проектов и выделить самый приемлемый. Показатель следует использовать в анализе вместе с рядом других показателей.
businessman.ru
Что такое индекс доходности? Как его рассчитать? :: SYL.ru
Стоит ли инвестировать свои средства, или нет? Дабы ответить на этот вопрос, необходимо предварительно рассчитать индекс доходности проекта. В таком случае инвестору не придется корить себя за принятие неверного решение при вложении капитала в предприятие, которое было заведомо убыточным.
Применение инвестиционного индекса доходности на начальной стадии
Индекс доходности инвестиций представляет собой показатель рентабельности инвестиционного проекта. Необходимо ознакомиться с порядком его расчета, чтобы правильно распорядиться средствами для инвестирования и в то же время свести риски к минимуму.
Индекс доходности PI представляет собой соотношение дисконтированных доходов и суммы инвестиций, сделаных на первом этапе. Для расчета требуется использовать следующую формулу:
Значение рассчитанного показателя должно превышать единицу. В таком случае можно признать проект потенциально эффективным.

Применение инвестиционного индекса доходности для готовых проектов
Однако рассматриваемую формулу желательно использовать лишь на начальной стадии создания проекта. Для определения рентабельности уже существующей компании предназначен более точный способ расчета. При этом применяются показатели чистого денежного потока за определенный период, первоначальных инвестиций и стоимость капитала, который был привечен для инвестиционного проекта.
С помощью данного способа можно рассчитать степень доходности для начального этапа, а также выявить, насколько точными оказались сведения раннего прогнозирования. С помощью расчета индекса рентабельности можно получить более точные данные, нежели с показателем чистого дисконтированного дохода. Особо уместно использование данного метода в тех ситуациях, когда инвестор делает выбор между несколькими объектами для вложений. В таком случае показатель PI покажет степень прибыльности каждого из них. При этом инвестор сможет выбрать наиболее подходящий вариант.

Расчет посредством данного метода имеет один значительный недостаток. Он заключается в том, что риск существует даже при значении PI > 1. При этом формулой не учитывается время, потраченное на реализацию проекта. Стоимость капитала может повыситься при изменении ставки рефинансирования ЦБ. Это станет причиной отрицательного дисконтирования.
Дисконтированный индекс доходности
Один из способов модификации понятия окупаемости инвестиций представляет собой суммирование имеющихся дисконтированных денежных потоков при их последующем делении на соответствующие инвестиционные расходы. В результате будет получен дисконтированный индекс доходности. Его также можно встретить под названием «отношение дохода к издержкам». Показатель выражается в текущей стоимости.

Вычисление дисконтированного индекса
Используется формула для выполнения расчета дисконтированного индекса доходности, в которой настоящая цена дохода от проекта делится на сумму капиталовложений. Для этого также могут потребоваться такие показатели:
- DPI – индекс доходности инвестиций, который рассчитывается долей единиц;
- CFt – денежный поток за определенный период времени;
- It – затраты на инвестиции за определенный период;
- r – ставка дисконтирования, выраженная в долях единиц;
- n – общее число учитываемых периодов.
Можно определить индекс доходности как отношение суммы всех дисконтированных доходов от инвестиций к соответствующим расходам. Он будет характеризовать рентабельность вложений, выраженную в относительных значениях. Если DPI > = 1,0, инвестиции будут вполне приемлемыми. Чем больше данный показатель, тем надежнее будет проект. Недостатком данного расчета эффективности вложения является отсутствие возможности сравнения денежных потоков с различной длительностью. К тому же нет точности в том, что доход будет получен по барьерной ставке.

Применение дисконтированного индекса доходности
Данный показатель могут использовать в экономике и управлении в таких случаях:
- Предстоит выбор между несколькими проектами.
- Анализируется экономическая ситуация в конкретном сегменте рынка.
- Анализируется рентабельность определенной компании или проекта.
- Необходимо рассчитать стоимость услуг и товаров, а также скорректировать ценовую политику компании при маленьком индексе доходности.
- Создаются прогнозы для развития бизнес-идей или проектов.
- Производится планирование бюджета компании, а также принятие решения о прекращении инвестирования или его продолжении.
- Выполняется разработка бизнес-плана и определение конкретных сроков реализации проектов и идей.
Потребоваться рассчитать индекс доходности инвестиций может и в других ситуациях.

Программы для выполнения расчета
Если определить индекс доходности вручную сложно, для этого можно использовать компьютерные программы. Калькуляция производится при введении необходимой функции в одной из простых программ, например Ms Excel.
Также существует специальное программное обеспечение. С его помощью легко выполнять сложные расчеты, а также строить графики, которые будут отражать ситуацию по исследуемому проекту. Данные функции частично доступны пользователям программы 1C для ведения бухгалтерского учета.
Правильный расчет дисконтированного индекса доходности позволит инвестору сделать правильный выбор между несколькими проектами и определить, будет ли выгодным вложение.
www.syl.ru
Задача №31. Расчёт индекса доходности и срока окупаемости инвестиций
Первоначальные инвестиции – 30 ед.
Срок амортизации – 5 лет.
Выручка от реализации по годам:
1-й год – 20 ед., 2-й – 22 ед., 3-й – 25 ед., 4-й – 24 ед., 5-й – 23 ед.
Текущие материальные издержки – 10 ед. и каждый год увеличиваются на 2 %.
Ставка налога на прибыль – 30 %.
Коэффициент дисконтирования – 0,1.
Определить индекс доходности и срок окупаемости инвестиций.
Решение:
Расходы по проекту состоят из суммы текущих материальных издержек и суммы амортизационных отчислений.
Ежегодные амортизационные отчисления рассчитаем линейным методом, в соответствии с которым ежегодная сумма амортизации определяется как отношение первоначальных инвестиций к сроку амортизации:
А = 30 / 5 = 6 ед.
Прибыль равна разности между выручкой и совокупными издержками:
П = Выручка – Расходы
В первом году прибыль будет равна:
П1 = 20 – (10 + 6) = 4
Рассчитаем сумму налога на прибыль в первом году:
СНП1 = П1 × t = 4 × 0,3 = 1,2
Тогда чистая прибыль в первом году будет равна:
ЧП1 = П1 – СНП1 = 4 – 1,2 = 2,8
Денежный поток (CF (Cash Flow)) первого года будет складываться из суммы чистой прибыли и суммы амортизационных отчислений:
CF1 = ЧП1 + А = 2,8 + 6 = 8,8
При расчёте денежного потока последующих лет необходимо учесть ежегодный прирост текущих материальных издержек на 2 %.
Оформим расчёты в таблицу:
| Период | IC | Bыручка | Расходы | Текущие материальные издержки | Амортизационные отчисления, (А) | Прибыль, (П) | Сумма налога на прибыль, (СНП) | Чистая прибыль, (ЧП) | Денежный поток, (CF) | Дисконтированный денежный поток |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 30 | — | — | — | — | — | — | — | — | — |
| 1 | — | 20 | 16 | 10 | 6 | 4 | 1,2 | 2,8 | 8,8 | 8 |
| 2 | — | 22 | 16,2 | 10,2 | 6 | 5,8 | 1,74 | 4,06 | 10,06 | 8,31 |
| 3 | — | 25 | 16,4 | 10,4 | 6 | 8,6 | 2,58 | 6,02 | 12,02 | 9,03 |
| 4 | — | 24 | 16,61 | 10,61 | 6 | 7,39 | 2,22 | 5,17 | 11,17 | 7,63 |
| 5 | — | 23 | 16,82 | 10,82 | 6 | 6,18 | 1,85 | 4,32 | 10,32 | 6,41 |
| Сумма | — | — | — | — | — | — | — | — | — | 39,38 |
Индекс доходности рассчитывают как отношение суммы приведенного (дисконтированного) чистого денежного потока от текущей деятельности за период осуществления проекта к общему объему капиталовложений:
ИД = 39,38 / 30 = 1,31
Значение индекса доходности 1,31 свидетельствует о экономической эффективности проекта, так как ИД>1.
Так как прибыль распределена неравномерно, то срок окупаемости рассчитывается прямым подсчетом числа лет, в течение которых чистые денежные поступления возместят инвестиционные затраты в проект.
| Период | CF | Кумулятивная сумма чистых денежных поступлений |
|---|---|---|
| 0 | — | — |
| 1 | 8,8 | 8,8 |
| 2 | 10,06 | 8,8 + 10,06 = 18,86 |
| 3 | 12,02 | 18,86 + 12,02 = 30,88 |
| 4 | 11,17 | 30,88 + 11,17 = 42,05 |
| 5 | 10,32 | 42,05 + 10,32 = 52,37 |
Срок окупаемости равен 3 годам, поскольку кумулятивная сумма чистых денежных поступлений за этот период (30,88) превышает объем капитальных вложений.
Однако некоторые специалисты более реальным сроком окупаемости считают дисконтированный срок окупаемости инвестиций. Суть метода заключается в дисконтировании всех денежных потоков, генерируемых проектом, и их последовательном суммировании до тех пор, пока не будут покрыты исходные инвестиционные затраты. Данный метод принимает в расчет стоимость денег во времени, что всегда показывает более реальную картину.
В данном случае дисконтированный срок окупаемости равен 4 годам.
| Период | Дисконтированный денежный поток | Кумулятивная сумма дисконтированных чистых денежных поступлений |
|---|---|---|
| 0 | — | — |
| 1 | 8 | 8 |
| 2 | 8,31 | 16,31 |
| 3 | 9,03 | 25,34 |
| 4 | 7,63 | 32,97 |
| 5 | 6,41 | 39,38 |
| Сумма | 39,38 | — |
ecson.ru