Калейдоскоп формул для пи
Калейдоскоп формул для пи«…я считал, что есть две математики — алгебраическая и геометрическая, и что геометрическая математика принципиально “трансцендентна” для алгебраической. Возьмите, например, формулу длины окружности — там есть “геометрическое” число $\pi$. Или, скажем, синус — он определяется чисто геометрически.
Когда я обнаружил, что синус можно записать алгебраически в виде ряда, барьер обрушился, математика стала единой.»
— из интервью И. М. Гельфанда
«Калейдоскоп» ниже состоит из нескольких «алгебраических» формул для $\pi$ с краткими комментариями. Он также опубликован (с сокращениями) в журнале «Квант» (№5 за 2020 год).
1. Формула Виета
Одна из первых алгебраических формул для $\pi$ — это открытое в XVI веке Виетом бесконечное произведение
$$
\frac\pi2=\frac2{\sqrt2}\cdot\frac2{\sqrt{2+\sqrt2}}\cdot\frac2{\sqrt{2+\sqrt{2+\sqrt2}}}\cdot\ldots
$$
Это равенство не очень сложно доказать. Идея состоит в следующем.
4. Формула Валлиса
Если подставить $x=\pi/2$ в разложение Эйлера синуса в бесконечное произведение, то получается равенство $$ \frac\pi2= \frac{2\cdot2\cdot4\cdot4\cdot6\cdot6\cdot\ldots}{1\cdot3\cdot3\cdot5\cdot5\cdot7\cdot\ldots} $$ Впрочем, Джон Валлис нашел эту формулу уже в середине XVII века, почти за 100 лет до формулы Эйлера, вычисляя некоторые интегралы.
В упоминавшейся выше статье Ягломов при помощи элементарной тригонометрии доказывается и формула Валлиса. А J. Wästlund нашел и доказательство (в духе «геометрического суммирования»), непосредственно связывающее произведение Валлиса с площадью круга — см. его статью (AMM, 2007) или лекцию Д. Кнута.
При помощи формулы Валлиса можно доказать, что если подкинуть монету $2n$ раз, то вероятность того, что орлов и решек выпадет в точности поровну, приблизительно равна $1/\sqrt{\pi n}$.
что это такое, чему равно, история, как округлить
Представляете, мы живем в эпоху технологического прорыва, но до сих пор не можем точно рассчитать площадь съеденного круглого торта? Все потому, что в формуле вычисления площади круга используется число π.
От автомобильного колеса до орбиты спутника, от часового механизма до электромагнитных и звуковых волн. В любой научной области есть расчеты, и практически в любом расчете не обойтись без числа пи. Даже там, где, казалось бы, окружности нет места, например в статистике.
Что такое число пи
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. Если записать это отношение математическими символами, то выглядит оно так: π = C/d, где C — это длина окружности, а d — диаметр окружности. То есть π — это результат деления длины окружности на ее диаметр. Но само по себе число пи не является каким-то параметром окружности. Это математическая постоянная, или константа (то есть неизменная), которая нужна для расчета определенных данных.
Например, число пи необходимо, чтобы посчитать площадь круга.
Чему равно число пи
Число пи не имеет точного значения. Это легко проверить. Возьмите круг любого размера, разделите его окружность на диаметр — у вас получится десятичная дробь с множеством цифр после запятой. Математики называют такие числа иррациональными. Результат, который вы увидите, будет равен 3 целых и сколько-то десятых, сотых, тысячных — и далее насколько хватит дисплея калькулятора. У числа пи бесконечное количество знаков после запятой. Но для удобства в расчетах используют округленные значения.
Число π примерно равно 3,14, или, если точнее, 3,1415926535. Именно значение с десятью знаками после запятой принято использовать. Но все дело в округлении. Там, где не нужны максимально точные расчеты, за число пи часто берут 3. А вот для точных расчетов в науке ученые используют число пи с 38-ю знаками десятичного разложения (после запятой в десятичной дроби).
Итак:
π = 3,14 или π = 3,1415926535
Как посчитать число пи самостоятельно
Возьмите несколько круглых предметов разного размера, например тарелку, блюдце и крышку от кастрюли.
Измерьте окружность каждого. Для этого используйте сантиметровую ленту. Или можно обернуть их по окружности ниткой или веревкой, а потом полученную длину нитки или веревки измерить линейкой. С помощью сантиметровой ленты или линейки измерьте и диаметр каждого предмета. Длина окружности и диаметры у каждого будут разные, ведь предметы разные по размеру.
Теперь для каждого предмета разделите его длину окружности на диаметр. Вы увидите, что во всех случаях, какого бы размера ни был круглый предмет, полученное значение будет 3 целых и далее десятые и сотые доли. Оно необязательно соответствует принятому значению в 3,14, но всегда будет около него.
Практическое применение числа пи
В школе нас учат использовать число пи для вычисления площади круга. Рассчитывается она по следующей формуле: S = πr², где S — площадь, π — число пи, r² — радиус в квадрате. Можно использовать эту формулу: S = d²/4*π, где d² — диаметр.
Зная число пи и диаметр, можно посчитать длину окружности.
Для этого вспомним школьные уравнения. Если π = C/d, то C (длина окружности) высчитывается по формуле C = π*d.
Но применение числа пи в науке гораздо шире. Оно используется практически для любых расчетов в любой области, будь то архитектура, авиация и даже статистика. Например, число π нужно для расчета времени полета самолета и расстояния, которое он должен преодолеть. А в статистике с помощью числа пи рассчитывают значения ниже так называемой кривой нормального распределения. Это нужно для того чтобы, например, выяснить, как распределялись голоса респондентов при опросе.
S (площадь круга) = πr²
История числа пи
Считается, что первым обозначать число пи буквой греческого алфавита π (pi) стал британский математик Уильям Джонс в 1706 году, а популяризировал обозначение его швейцарский коллега Леонард Эйлер в 1737 году. Есть версия, что эта буква выбрана не случайно, а как начальная в греческом слове perijereia, что означает «окружность», «периферия».
Как и на многие явления, известные науке сегодня, на существование некой постоянной, с помощью которой можно посчитать площадь круга, обратили внимание еще в Древнем мире.
Но ученые того времени приходили к разному мнению относительно значения этой постоянной: одни использовали значение 3,125, другие — 3,16, третьи — 3,139. Но всегда это значение было 3 с небольшим.
На точное вычисление числа пи ушли тысячелетия. Первым, кто определил более-менее приблизительное значение π, был древнегреческий ученый Архимед. По его расчетам пи равно 3,142857142857143. Как мы знаем сейчас, верными оказались только первые два десятичных числа.
это интересно
Натуральные числа
Их разряды, классы и свойства
подробнееТочнее оказались расчеты китайского математика 480-х годов нашей эры — 3,1415927. Именно это значение числа пи считалось самым верным до 1420-х годов, пока ученые не расширили этот ряд до 16 цифр после запятой, затем до 20-ти, 32-х и так далее.
В XX веке с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины. С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).
Популярные вопросы и ответы
Отвечают Вячеслав Смольняков, учитель математики и информатики высшей квалификационной категории, эксперт ОГЭ и ЕГЭ Региональной предметной комиссии по математике и информатике; Ирина Ходакова, учитель математики.
Как округлить число пи?
Чтобы не запоминать число пи с большим количеством десятичных значений, его принято округлять, — говорит Вячеслав Смольняков. — В математике все округления проводятся по строгим правилам. Для округления значения числа пи применяют метод округления к ближайшему целому. Если перед округляемым числом стоит число 5 и большее, то число округляется в большую сторону. Например, 12,513. Другой пример: 12,5812,613.Если перед округляемым числом стоит число менее 5, то число округляется в меньшую сторону. Например, 12,412. Или: 12,3412,312.
Итак, возьмем π — 3,1415. Округление начинают с последнего значения, в данном случае это 5. Значит, следующая за ним единица округляется до двух: 3,14153,142.
Последнее число 2 меньше пяти, значит, последующее 4 остается неизменным: 3,1423,14. Вот мы и пришли к общепринятому значению числа пи.
По тому же принципу давайте продолжим округление до целого числа: 3,143,23. И вот у нас получилось значение числа пи 3.
Как запомнить число пи?
Чтобы запомнить значение числа π, — советует Ирина Ходакова, — используют один из самых популярных способов — запомнить фразу, в которой количество букв в каждом слове совпадает с цифрами числа π.Например, «Что(3) я(1) знаю(4) о(1) круге(5)?»
Чтобы запомнить больше знаков числа π, пользуются различными приемами мнемотехники (совокупность приемов, облегчающих запоминание информации). Например, существует стихотворение С. Боброва «Волшебный двурог» для запоминания числа π, которое совсем не сложно выучить:
«Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим —
Это будет пять, три, пять,
Восемь, девять, восемь»
Где используется число пи?
Изначально число π было необходимо для применения в строительстве.
Ведь порой из-за погрешности в значении числа π падали башни и рушились целые дворцы. Сейчас π используется в различных сферах нашей жизни.Мы уже выяснили, что число π позволяет нам рассчитывать и создавать окружности. Если колеса на вашем автомобиле будут немного отличаться друг от друга, то поездки для вас станут как минимум не очень удобными. Но применение числа π этим не ограничивается. Например, без числа π нельзя было бы обеспечить качественную работу телевизоров, радио и телефонов, так как инженеры используют π для расчета и оптимизации звуковых волн. Также π играет важную роль в расчете времени и расстояния путешествия на самолете, так как на большие расстояния самолеты летят по округлой дуге. Не было бы даже многих игр, таких как футбол, баскетбол, теннис, ведь мячи должны быть абсолютно круглыми.
Значение числа Пи в математике
Значение числа Пи (π) представляет собой отношение длины окружности к ее диаметру и приблизительно равно 3,14159 .
В круге, если вы разделите длину окружности (это общее расстояние по окружности) на диаметр, вы получите точно такое же число. Независимо от того, большой круг или маленький, значение числа Пи остается неизменным. Символ Пи обозначается π и произносится как «пирог». Это 16-я буква греческого алфавита, используемая для обозначения математической константы.
Значение Пи
Значения Пи в десятичных и дробных числах
Pi (или π) в основном выражается двумя разными способами:
- Значение числа пи в десятичном формате
- Значение числа пи в дроби
Десятичное число Пи (π)
Число Пи до первых 100 знаков после запятой:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 7067
Значение числа Пи (π) в дробях
Число пи в дроби равно 22/7. Известно, что пи — иррациональное число, а это означает, что цифры после запятой бесконечны и являются неконечным значением.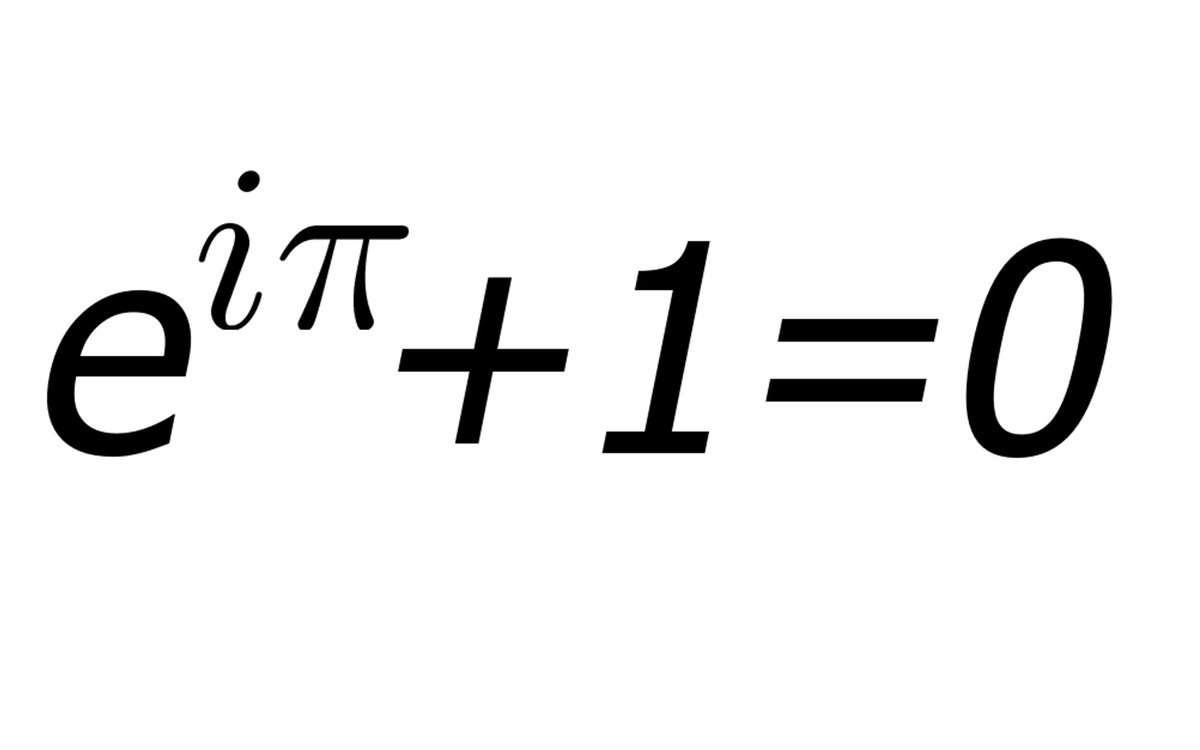
Поэтому для повседневных вычислений используется режим 22/7. « π» не равно отношению любых двух чисел, что делает его иррациональным числом.
| Все значения Пи (π) | |
|---|---|
| Десятичный | 3,14 |
| Во Фракции | 22⁄7 |
Как рассчитать число Пи? (Формула Пи)
Для вычисления значения π используется формула Пи, которая равна:
π = (окружность/диаметр)
Или π = 3,14159 = 22/7
Примеры использования числа Пи
Вопрос 1: Мальчик идет по кругу диаметром 100 м, какое расстояние прошел мальчик?
Решение:
Пройденное расстояние = Окружность.
Окружность = π × 100 м = 314,159 м
Следовательно, пройденное расстояние = 314,159 м
Вопрос 2: Вычислите длину окружности.
Решение:
Мы знаем, что длина окружности — это расстояние по окружности.
Формула длины окружности задается как c = π × d.
Следовательно, при подстановке значения d получаем;
С = π х 18
=3,14 х 18
= 56,52 см
Посмотрите видео ниже, чтобы узнать ценность числа Пи и его силу
Изучите другие математические концепции простым и эффективным способом, посетив BYJU’S и загрузив приложение.
Часто задаваемые вопросы
Q1
Каково точное значение числа Пи и почему?
Число «пи» является иррациональным числом и не имеет точного значения. Обычно значение π считается равным 3,14 или 22/7 для различных математических расчетов.
Q2
Что такое число Пи и как оно появилось?
Пи — математическая константа, представляющая отношение длины окружности к диаметру круга. Число Пи было впервые вычислено Архимедом Сиракузским. Символ π впервые популяризировал Леонард Эйлер в 1737 году.
Q3
По какой формуле вычисляется число pi?
Пи — это отношение, полученное из окружности.
Если диаметр и длина окружности известны, значение числа пи будет следующим: π = длина окружности/диаметр.
Пи — Что такое Формула Пи? Примеры
Формула Пи связывает длину окружности и диаметр круга. Его можно использовать для вычисления значения числа пи, если даны измерения окружности и диаметра круга. Пи — это греческая буква, ее символ — π, а в геометрии — это отношение длины окружности любого круга к диаметру этого круга. В десятичной форме значение числа пи составляет приблизительно 3,14159… Его нельзя записать в виде точной десятичной дроби, поскольку в нем есть цифры, которые идут бесконечно. Давайте узнаем о формуле Пи с несколькими решенными примерами в конце.
Что такое формула Пи?
Пи, будучи иррациональным числом, не может быть выражено в виде обыкновенной дроби. Хотя для ее приближения обычно используются такие дроби, как 22/7, точное значение числа пи, которое представляет собой непрерывающуюся неповторяющуюся десятичную дробь, можно рассчитать с помощью формулы числа пи.
Независимо от того, насколько большой или маленький круг, длина окружности, деленная на диаметр круга, всегда π. Формула Пи может быть выражена следующим образом:
Формула Пи (π) = (Диаметр окружности / Диаметр)
Другие формулы с числами Пи
В геометрии есть некоторые основные формулы, содержащие число Пи. Формулы таковы:
- Периметр круга равен 2πr.
- Площадь круга πr 2 .
- Объем сферы 4/3πr 3 .
- Площадь поверхности сферы 4πr 2 .
Где «r» – радиус круга или сферы.
Давайте взглянем на несколько примеров решения формулы Пи, чтобы лучше понять концепцию.
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Заказать бесплатный пробный урок
Примеры по формуле числа Пи
Пример 1: Ной измерил периметр круглого сечения трубы как 88 дюймов.
Рассчитайте диаметр той же трубы по формуле Пи. (Используйте π = 3,14 )
Решение:
Найти: Диаметр трубы.
Периметр круглой трубы = 88 дюймов (дано) 90 183
Используя формулу Пи,
Pi(π) = (Диаметр окружности)
3,14 = (88/диаметр)
Диаметр = (88/3,14)
= 28,02
= 28 дюймов (прибл.).
Ответ: диаметр трубы составляет 28 дюймов (приблизительно).
Пример 2: Диаметр круглого парка составляет 200 дюймов. Используя формулу Пи, рассчитайте, какое расстояние вы преодолели, если прошли ровно 1 круг через его границу. (Используйте π = 3,14)
Решение:
Найти: Окружность парка.
Диаметр парка = 200 дюймов.
Pi(π) = (Диаметр окружности)
3,14 = (окружность / 200)
Окружность = (3,14 × 200) дюймов.
= 628 дюймов
Ответ: Общее пройденное расстояние равно 628 дюймов.
Пример 3: Джеймс измерил периметр круга как 66 единиц, а диаметр того же круга равен 21 единице.
