Документальное оформления договора факторинга с регрессом
16.12.2009
Один из двух покупателей не оплатил в срок долг за поставленный товар. Банк в безакцептном порядке взыскал сумму задолженности с ИП согласно условиям договора факторинга. ИП применяет общую систему налогообложения (кассовый метод).
Какой порядок отражения в книге учета доходов и расходов всех операций по договору факторинга?
Какой порядок документального оформления данных операций (всех)?
Как отразится в налоговом учете ИП предъявление покупателю претензии?
Рассмотрев вопрос, мы пришли к следующему выводу:
Договор факторинга с регрессом сочетает в себе элементы договора займа под обеспечение правами требования и договора оказания услуг в виде администрирования банком (фактором) дебиторской задолженности.
Таким образом, по нашему мнению, поступление средств от фактора в виде финансирования в размере 90% от стоимости прав требования в Книге учета не отражается.
Доход от реализации товара в размере 100% дебиторской задолженности, погашенной покупателем фактору, должен быть отражен в Книге учета в момент получения от фактора отчета и перечисления им оставшихся 10% от стоимости прав требования. Одновременно отражается прочий расход в виде вознаграждения фактора.
Обоснование вывода:
Сначала выясним правовой характер факторинга с регрессом. Факторинг является разновидностью финансирования под уступку права требования, которому посвящена глава 43 ГК РФ (ст.ст. 824-833 ГК РФ). Следует отметить, что права требования являются частью имущества организации (п. 2 ст. 132 ГК РФ), которым можно распорядится по своему усмотрению — реализовать, использовать в качестве залога и т.
В соответствии со ст. 824 ГК РФ по договору финансирования под уступку денежного требования (договору факторинга) одна сторона (финансовый агент) передает или обязуется передать другой стороне (клиенту) денежные средства в счет денежного требования клиента (кредитора) к третьему лицу (должнику), вытекающего из предоставления клиентом товаров, выполнения им работ или оказания услуг третьему лицу, а клиент уступает или обязуется уступить финансовому агенту это денежное требование. При этом в п. 3 ст. 827 ГК РФ указано, что договором факторинга может быть предусмотрена ответственность клиента за неисполнение или ненадлежащее исполнение должником требования, являющегося предметом уступки, в случае предъявления его финансовым агентом к исполнению (так называемый факторинг с регрессом или оборотный факторинг).
Кроме того, п. 2 ст. 831 ГК РФ предусмотрено, что если уступка денежного требования финансовому агенту осуществлена в целях обеспечения исполнения ему обязательства клиента и договором финансирования под уступку требования не предусмотрено иное, финансовый агент обязан представить отчет клиенту и передать ему сумму, превышающую сумму долга клиента, обеспеченную уступкой требования.
Если денежные средства, полученные финансовым агентом от должника, оказались меньше суммы долга клиента финансовому агенту, обеспеченной уступкой требования, клиент остается ответственным перед финансовым агентом за остаток долга.
Таким образом, факторинг с регрессом означает, что финансовый агент финансирует (кредитует) клиента с условием о том, что в качестве обеспечения возврата денег он принимает уступленное клиентом право требования долга к третьему лицу.
Такая форма обеспечения предусмотрена п. 1 ст. 329 ГК РФ и абзацем вторым п. 1 ст. 824 ГК РФ, который устанавливает, что требование к должнику может быть уступлено в целях обеспечения обязательств клиента перед финансовым агентом. То есть в ситуации, когда должник не оплачивает свой долг в указанный срок, клиент должен вернуть финансовому агенту полученное финансирование, а затем самостоятельно получить долг с должника.
То есть договор факторинга с регрессом состоит из элементов договора займа (кредитного договора) и договора залога прав требования.
При заключении такого вида договора право требования передается финансовому агенту для обеспечения исполнения обязательств клиента по возврату полученного им займа или кредита. То есть право собственности на право требования остается у клиента, а не переходит финансовому агенту. В подтверждение такого вывода можно привести положения п. 1 ст. 831 ГК РФ, который относится к факторингу без регресса. Согласно п. 1 ст. 831 ГК РФ, если по условиям договора финансирования под уступку денежного требования финансирование клиента осуществляется путем покупки у него этого требования финансовым агентом, последний приобретает право на все суммы, которые он получит от должника во исполнение требования, а клиент не несет ответственности перед финансовым агентом за то, что полученные им суммы оказались меньше цены, за которую агент приобрел требование. Таким образом, сравнивая положения п. 1 с п. 2 ст. 831 ГК РФ, можно прийти к выводу, что факторинг без регресса предусматривает финансирование путем покупки прав требования, а факторинг без регресса предусматривает финансирование под обеспечение правами требования.
Суды при квалификации договора факторинга с регрессом также приходят к выводу о смешанном характере такого договора, содержащего элементы, в том числе, договора займа и договора возмездного оказания услуг. В связи с этим существуют основания для применения к отношениям сторон по такому договору в соответствующей части положений параграфа 1 главы 42 «Заем» ГК РФ (постановление ФАС Поволжского округа от 20.11.2008 N А55-2337/2008). Дело в том, что п.п. 1-4 ст. 421 ГК РФ установлена свобода сторон в заключении договора. Так, стороны могут заключить договор, в котором содержатся элементы различных договоров, предусмотренных законом или иными правовыми актами (смешанный договор).
Таким образом, по нашему мнению, договор факторинга с регрессом несет в себе элементы договора займа (в виде финансирование банком под залог прав требования) и договора возмездного оказания услуг. Отчет, оформляемый в соответствии с п. 2 ст.
Учет операций по договору факторинга с регрессом
В соответствии со ст. 4 Федерального закона от 21.11.1996 N 129-ФЗ «О бухгалтерском учете» граждане, осуществляющие предпринимательскую деятельность без образования юридического лица, ведут учет доходов и расходов в порядке, установленном налоговым законодательством РФ. Таким образом, индивидуальные предприниматели ведут только налоговый учет.
В соответствии с п. 2 ст. 54 НК РФ индивидуальные предприниматели (далее — ИП) исчисляют налоговую базу по итогам каждого налогового периода на основе данных учета доходов и расходов и хозяйственных операций в порядке, определяемом Минфином России. Данный порядок утвержден приказом Минфина России и МНС РФ от 13.08.2002 N 86н/БГ-3-04/430 «Об утверждении Порядка учета доходов и расходов и хозяйственных операций для индивидуальных предпринимателей» (далее — Порядок).
В соответствии с п. 4 Порядка учет доходов и расходов и хозяйственных операций ведется ИП путем фиксирования в Книге учета доходов и расходов и хозяйственных операций индивидуального предпринимателя (далее — Книга учета) операций о полученных доходах и произведенных расходах в момент их совершения на основе первичных документов позиционным способом.
В соответствии с п. 13 Порядка доходы и расходы отражаются в Книге учета кассовым методом, то есть после фактического получения дохода и совершения расхода, за исключением случаев, предусмотренных Порядком. В связи с этим предъявление претензии покупателю никаким образом не отразится в Книге учета, поскольку не происходит движения денежных средств.
В соответствии с п. 14 Порядка в доход включаются все поступления от реализации товаров, выполнения работ и оказания услуг, а также стоимость имущества, полученного безвозмездно.
А согласно п.
15 Порядка под расходами понимаются фактически произведенные и документально подтвержденные затраты, непосредственно связанные с извлечением доходов от предпринимательской деятельности.
Таким образом, учитывая правовую природу факторинга с регрессом, считаем, что операции, связанные с исполнением такого договора, должны отражаться в Книге учета в следующем порядке:
1) отгрузка товара покупателям не отражается в Книге учета, поскольку отсутствует поступление денежных средств;
2) поступление от фактора финансирования в размере 90% от стоимости прав требования, переданных ему в обеспечение, также не отражается в Книге учета, поскольку не является поступлением от реализации;
3) при получении от фактора оставшихся 10% стоимости прав требования, переданных ему в обеспечение, а также при получении от фактора отчета, в Книге учета отражается доход от реализации в размере 100% суммы погашенной покупателем задолженности;
4) одновременно в Книге учета отражаются прочие расходы в виде вознаграждения фактора.
Однако обращаем внимание на отсутствие официальных разъяснений, подтверждающих или опровергающих наш вывод. В связи с этим рекомендуем обратиться за разъяснениями в Минфин России с описанием конкретной ситуации (пп. 2 п. 1 ст. 21 НК РФ). Так, согласно п. 3 ст. 34.2 НК РФ Минфин России финансовые органы субъектов РФ и муниципальных образований дают письменные разъяснения в пределах своей компетенции в течение двух месяцев со дня поступления соответствующего запроса.
Эксперты службы Правового консалтинга ГАРАНТ Ткач Ольга, Родюшкин Сергей
Статьи по теме
ГАРАНТ: требуется ли гос.
регистрация договора цессии на недвижимость
09.08.2022
Подробнее
Эксперты ГАРАНТа разъяснили порядок начисления процентов при переуступке права требования долга
31.07.2021
Подробнее
Эксперты ГАРАНТа перечислили перечень документов для отражения в учете перевода задолженности при факторинге
09.12.2021
Подробнее
ГАРАНТ: требуется ли гос.регистрация договора цессии на недвижимость
09.08.2022
Подробнее
Эксперты ГАРАНТа разъяснили порядок начисления процентов при переуступке права требования долга
31.07.2021
Подробнее
Эксперты ГАРАНТа перечислили перечень документов для отражения в учете перевода задолженности при факторинге
09.
12.2021
Подробнее
Комментарий к статье 824. ГК РФ
1. Финансирование под уступку денежного требования является новым для отечественного гражданского права институтом.
Вместе с тем подобные операции известны многим зарубежным правопорядкам и получили широкое распространение в международной торговой практике. Их унифицированное правовое регулирование содержится в рамках Оттавской конвенции УНИДРУА о международном факторинге 1988 г. (далее — Конвенция о факторинге), а также Конвенции ООН об уступке дебиторской задолженности в международной торговле 2001 г. (далее — Конвенция ООН об уступке). Хотя Россия не участвует в указанных международных договорах, большинство их норм и принципов либо непосредственно восприняты отечественным правопорядком и нашли свое закрепление в рамках гл. 43 ГК, либо могут использоваться в качестве ориентира при толковании и применении соответствующих законодательных положений.
2. В юридической литературе рассматриваемый договор зачастую именуется факторингом.
Между тем в настоящее время факторинг представляет собой лишь одну из возможных форм финансирования под уступку требования наряду с форфейтингом, проектным финансированием, секьюритизацией, рефинансированием (подробнее см.: Ефимова Л.Г. Банковские сделки. Комментарий законодательства и арбитражной практики. М., 2000. С. 243 — 248; Новоселова Л.А. Сделки уступки права (требования) в коммерческой практике. Факторинг. М., 2004. С. 339 — 341).
Правила гл. 43 ГК имеют значение общих положений относительно всех указанных выше форм финансирования под уступку денежного требования.
3. Одним из основных элементов договора финансирования под уступку денежного требования является уступка права требования. Поэтому даже в отсутствие специальной нормы правила § 1 гл. 24 ГК о цессии подлежат применению к рассматриваемому договору, если они не противоречат положениям гл. 43 ГК.
4. В п. 1 коммент. ст. сформулировано определение договора финансирования под уступку денежного требования.
Данный договор может быть заключен как по модели консенсуального (когда обе стороны принимают на себя обязанности соответственно по передаче денежных средств и по уступке денежного требования), так и по модели реального договора.
Консенсуальный договор финансирования под уступку требования является взаимным. Что касается реального договора, то он по общему правилу носит односторонний характер (исключение составляют случаи, предусмотренные п. 2 коммент. ст. 824 ГК, когда договором на финансового агента возлагаются обязанности по оказанию клиенту дополнительных услуг).
Рассматриваемый договор является возмездным, поскольку исполнение каждой из сторон своих обязанностей обусловлено встречным имущественным предоставлением контрагента. При этом в качестве вознаграждения финансового агента выступает разница («дисконт») между номинальной стоимостью уступаемого клиентом требования и размером предоставляемого финансирования.
5. В рамках рассматриваемого договора денежные требования обычно уступаются финансовому агенту в обмен на предоставление клиенту соответствующих денежных средств, выступая, по сути, в качестве способа возврата клиентом кредита (схема «покупки»).
Наряду с этим абз. 2 п. 1 коммент.
ст. предусматривает возможность использования уступки денежного требования и в качестве способа обеспечения исполнения обязательств клиента перед финансовым агентом (схема «обеспечения») (см. коммент. к ст. 831 ГК).
6. Предметом рассматриваемого договора являются, с одной стороны, денежные средства, передаваемые клиенту, а с другой — денежное требование клиента к третьему лицу, которое уступается финансовому агенту.
В рамках договора финансирования возможна уступка лишь денежных требований, вытекающих из договора (см. коммент. к ст. 826 ГК). Возмездное отчуждение иных имущественных прав (если оно принципиально возможно с учетом их характера) опосредуется иными договорами, в частности куплей-продажей.
Круг существенных условий договора финансирования ограничивается лишь условием о предмете. Отсутствие в конкретном договоре иных условий не влечет признания его незаключенным и должно восполняться с помощью общих правил об обязательствах (гл. 22 ГК).
7. Помимо основной обязанности по предоставлению финансирования, договором на финансового агента может быть возложено оказание клиенту дополнительных финансовых и коммерческих услуг, например ведение бухгалтерского учета, обработка и выставление счетов и т.
п. (п. 2 коммент. ст.). Договор, содержащий подобные условия, следует считать смешанным, а к отношениям сторон применять наряду с правилами гл. 43 ГК нормы о возмездном оказании услуг (поручении, агентировании и проч.).
По смыслу коммент. ст. оказание дополнительных услуг является не обязательным, а лишь факультативным элементом рассматриваемого договора. Обязанности финансового агента могут ограничиваться лишь предоставлением финансирования. В этом вопросе ГК не воспринял положения Конвенции о факторинге, ст. 1 которой предусматривает возложение на финансового агента по меньшей мере двух из следующих функций: финансирование поставщика; ведение учета по причитающимся суммам; предъявление к оплате денежных требований; защита от неплатежеспособных должников.
8. Содержащееся в коммент. ст. определение договора финансирования, к сожалению, не позволяет однозначно определить признаки, на основании которых возможно разграничение между рассматриваемым договором и другими договорными конструкциями, в рамках которых возможна передача права требования (в частности, куплей-продажей).
В доктрине этот вопрос также не получил однозначного решения (см., например: Брагинский М.И., Витрянский В.В. Договорное право. Книга пятая: В 2 т. Т. 1. Договоры о займе, банковском кредите и факторинге. Договоры, направленные на создание коллективных образований. М., 2006. С. 542 — 548 (автор главы — В.В. Витрянский)). Такая неопределенность порождает сложности в правоприменительной деятельности, не способствует развитию отношений финансирования под уступку требования и должна быть устранена законодателем. В качестве квалифицирующих для рассматриваемого договора целесообразно было бы использовать признаки, указанные в ст. 1 Конвенции о факторинге.
Имитационное исследование радиочастотной безопасности и оптимального размера одноканальной поверхностной радиочастотной катушки для мышей при магнитно-резонансной томографии 9,4 Тл
1. Корецкий А.П. Изучение клеточного энергетического метаболизма у трансгенных мышей. Физиол. 1995; 75:667–688. doi: 10.1152/physrev.1995.75.4.
667. [PubMed] [CrossRef] [Google Scholar]
2. Christensen G., Wang Y., Chien K.R. Физиологическая оценка сложных сердечных фенотипов у генетически модифицированных мышей. Являюсь. Дж. Физиол. 1997;272:h3513–h3524. doi: 10.1152/ajpheart.1997.272.6.h3513. [PubMed] [CrossRef] [Google Scholar]
3. Джеймс Дж. Ф., Хьюитт Т. Е., Роббинс Дж. Физиология сердца у трансгенных мышей. Цирк. Рез. 1998; 82: 407–415. doi: 10.1161/01.RES.82.4.407. [PubMed] [CrossRef] [Google Scholar]
4. Roman B.B., Goldspink P.H., Spaite E., Urboniene D., McKinney R., Geenen D.L., Solaro R.J., Buttrick P.M. Ингибирование PKC фосфорилирования cTnI улучшает работу сердца in vivo. Являюсь. Дж. Физиол. Цирк Сердца. Физиол. 2004;286:h3089–h3095. doi: 10.1152/ajpheart.00582.2003. [PubMed] [CrossRef] [Google Scholar]
5. Benveniste H., Blackband S. МР-микроскопия и МРТ мелких животных с высоким разрешением: применение в исследованиях в области неврологии. прог. Нейробиол. 2002; 67: 393–420. doi: 10.
1016/S0301-0082(02)00020-5. [PubMed] [CrossRef] [Google Scholar]
6. Cantley M.D., Bartold P.M., Marino V., Reid R.C., Fairlie D.P., Wyszynski R.N., Zilm P.S., Haynes D.R. Использование микрокомпьютерной томографии на живых животных для определения влияния нового ингибитора фосфолипазы А2 на потерю альвеолярной кости в мышиной модели периодонтита in vivo. J. Периодонтальная рез. 2009 г.;44:317–322. doi: 10.1111/j.1600-0765.2008.01132.x. [PubMed] [CrossRef] [Google Scholar]
7. Kim Y., Hamada N., Takahashi Y., Sasaguri K., Tsukinoki K., Onozuka M., Sato S. Шейная симпатэктомия вызывает потерю альвеолярной кости в эксперименте. модель крысы. J. Периодонтальная рез. 2009; 44: 695–703. doi: 10.1111/j.1600-0765.2008.01177.x. [PubMed] [CrossRef] [Google Scholar]
8. Marques M.R., dos Santos M.C., da Silva A.F., Nociti F.H., Barros S.P., Jr. Введение паратиреоидного гормона может модулировать уровни интерлейкина-6 и матриксной металлопротеиназы-2 в тканях пародонта. и матриксная металлопротеиназа-9при экспериментальном пародонтите.
J. Периодонтальная рез. 2009; 44: 744–750. doi: 10.1111/j.1600-0765.2008.01186.x. [PubMed] [CrossRef] [Google Scholar]
9. Полак Д., Виленский А., Шапира Л., Халаби А., Гольдштейн Д., Вайс Э.И., Хури-Хаддад Ю. Мышиная модель экспериментального пародонтита, индуцированного Porphyromonas gingivalis/Fusobacterium nucleatum: потеря костной массы и реакция хозяина. Дж. Клин. Пародонтол. 2009; 36: 406–410. doi: 10.1111/j.1600-051X.2009.01393.x. [PubMed] [CrossRef] [Академия Google]
10. Фернандес Л.А., де Алмейда Дж.М., Теодоро Л.Х., Боско А.Ф., Нагата М.Дж., Мартинс Т.М., Окамото Т., Гарсия В.Г. Лечение экспериментального пародонтита фотодинамической терапией у крыс с подавленным иммунитетом. Дж. Клин. Пародонтол. 2009; 36: 219–228. doi: 10.1111/j.1600-051X.2008.01355.x. [PubMed] [CrossRef] [Google Scholar]
11. Queiroz-Junior C.M., Pacheco C.M., Maltos K.L., Caliari M.V., Duarte I.D., Francischi J.N. Роль системного и местного введения селективных ингибиторов циклооксигеназы 1 и 2 в экспериментальной модели пародонтита у крыс.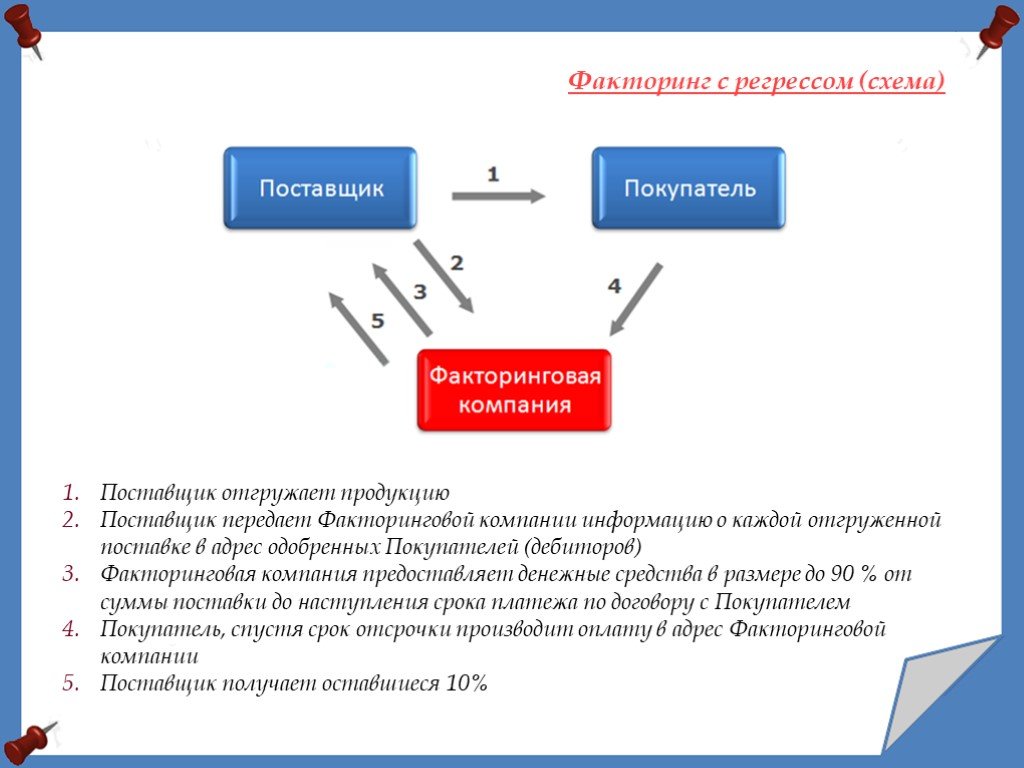
J. Периодонтальная рез. 2009 г.;44:153–160. doi: 10.1111/j.1600-0765.2007.01069.x. [PubMed] [CrossRef] [Google Scholar]
12. Марзола П., Оскулати Ф., Сбарбати А. МРТ высокого поля в доклинических исследованиях. Евро. Дж. Радиол. 2003; 48: 165–170. doi: 10.1016/j.ejrad.2003.08.007. [PubMed] [CrossRef] [Google Scholar]
13. Leynes A.P., Chen Y., Sukumar S., Xu D., Zhang X. Компактная планарная трехядерная катушка для мелких животных 1 H, 13 C и 31 P МРТ метаболизма при 14,1 T. arXiv. 20212109.03015 [Google Scholar]
14. Славсон С.Э., Роман Б.Б., Уильямс Д.С., Корецкий А.П. МРТ нормального и гипертрофированного сердца мыши. Магн. Резон. Мед. 1998; 39: 980–987. doi: 10.1002/mrm.19103
. [PubMed] [CrossRef] [Google Scholar]
15. Ким К.-Н., Сео Дж.-Х., Хан С.-Д., Хео П., Им Г.Х., Ли Дж.Х. Разработка двухслойной связанной катушки для улучшения отношения сигнал-шум в МРТ мелких животных 7 Тл. Сканирование. 2015; 37: 361–371.
doi: 10.1002/sca.21217. [PubMed] [CrossRef] [Академия Google]
16. Gatto R.G., Weissmann C. Предварительное исследование ранних признаков нейроконнективности в мышиной модели болезни Гентингтона R6/1 с помощью МРТ с диффузией в сверхвысоком поле. Нейронная регенерация. Рез. 2022; 17: 983–986. doi: 10.4103/1673-5374.324831. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
17. Zhu X.H., Chen W. Методы рентгеновской МРС-визуализации in vivo для количественной оценки нейроэнергетических биомаркеров при изучении функции мозга и старения. Передний. Стареющие нейроски. 2018;10:394. doi: 10.3389/fnagi.2018.00394. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
18. Ниндорф Т., Польманн А., Райманн Х.М., Вайциес Х., Пепер Э., Хюльнхаген Т., Зелигер Э., Шрайбер А., Кеттриц Р., Стробел К. и др. Улучшение сердечно-сосудистой, нейроваскулярной и почечной магнитно-резонансной томографии у мелких грызунов с использованием технологии криогенной радиочастотной катушки.
Передний. Фармакол. 2015;6:255. doi: 10.3389/fphar.2015.00255. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
19. Оз Г., Ткач И., Угурбил К. Модели животных, высокопольная визуализация и спектроскопия. Диалоги клин. Неврологи. 2013; 15: 263–278. doi: 10.31887/DCNS.2013.15.3/goz. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
20. Chi Z., Yi Y., Wang Y., Wu M., Wang L., Zhao X., Meng Y., Zheng Z. , Чжао К., Чжоу Дж. Адаптивные цилиндрические беспроводные метаповерхности в клинической магнитно-резонансной томографии. Доп. Матер. 2021;33:2102469. doi: 10.1002/adma.202102469. [PubMed] [CrossRef] [Академия Google]
21. Махмуд М.Ф., Гарган С.К., Мохаммед С.Л., Аль-Наджи А., Чахл Дж. Конструкция питания беспроводного медицинского датчика на основе спирально-паутинных катушек. Дизайн. 2021;5:59. doi: 10.3390/designs5040059. [CrossRef] [Google Scholar]
22. Парк Б.С., Раджан С.С., Макрайт Б. Улучшение чувствительности и однородности МРТ-изображений с фазированной решеткой с использованием индуктивной связи и схем РЧ-расстройки.
Магн. Резон. Матер. физ. биол. Мед. 2020; 33: 725–733. [PubMed] [Google Scholar]
23. Пак Б.С., Ма Г., Кох В.Т., Раджан С.С., Мастроманолис М., Лам Дж., Сун К., Макрайт Б. Улучшение 19F Однородность МР-изображения в мышиной модели клеточной терапии с использованием индуктивной связи. Магн. Резон. Матер. физ. биол. Мед. 2019;32:15–23. doi: 10.1007/s10334-018-0693-9. [PubMed] [CrossRef] [Google Scholar]
24. Seo J.-H., Lee J.J., Kim K.-N. Поверхностная катушка с индуктивно связанной беспроводной поверхностной и объемной катушкой для улучшения чувствительности к магнитному полю при МРТ с частотой 400 МГц. Дж. Магн. 2018;23:192–195. doi: 10.4283/JMAG.2018.23.2.192. [CrossRef] [Google Scholar]
25. Булумулла С. Б., Файвлэнд Э., Парк К. Дж., Фу Т. К., Харди С. Дж. Массивы беспроводных катушек с индуктивной связью. Магн. Резон. Визуализация. 2015; 33: 351–357. [PubMed] [Академия Google]
26. Метт Р.Р., Сидабрас Дж.В., Хайд Дж.С. Пара «поверхность-катушка» МРТ с сильной индуктивной связью.
преподобный наук. Инструм. 2016;87:124704. doi: 10.1063/1.4972391. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
27. Ван Т., Чобану Л., Чжан С., Уэбб А. Конструкция РЧ-катушки с индуктивной связью для одновременного микроизображения нескольких образцов. Концепции Маг. Резон. Часть B Magn. Резон. англ. 2008; 33Б: 236–243. doi: 10.1002/cmr.b.20122. [CrossRef] [Google Scholar]
28. Kell R.C., Greenham A.C., Olds G.C.E. Термостабильные керамические диэлектрики с высокой диэлектрической проницаемостью и низкими микроволновыми потерями. Являюсь. Керам. соц. 1973;56:352–354. doi: 10.1111/j.1151-2916.1973.tb12684.x. [CrossRef] [Google Scholar]
29. Seo J.-H., Han Y. и Chung J.-Y. Сравнительное исследование конфигураций радиочастотных катушек с птичьей клеткой для магнитно-резонансной томографии сверхвысокого поля. Датчики. 2022;22:1741. doi: 10.3390/s22051741. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
30. Воробьев В., Щелокова А., Живкович И.
, Слобожанюк А., Баена Дж. Д., Риско Дж. П., Абдеддайм Р., Уэбб А., Глыбовский S. Плита из искусственного диэлектрика для МРТ со сверхвысоким полем: доказательство концепции. Дж. Магн. Резон. 2020;320:106835. doi: 10.1016/j.jmr.2020.106835. [PubMed] [CrossRef] [Академия Google]
31. Живкович И., Тиувисси В., Слобожанюкб А., Ненашевац Э., Уэбб А. Керамика с высокой диэлектрической проницаемостью улучшает передающее поле и эффективность приема коммерческой конечной катушки при 1,5 Тл. Дж. Магн. Резон. 2019;299:59–65. doi: 10.1016/j.jmr.2018.12.013. [PubMed] [CrossRef] [Google Scholar]
32. Lee B.-Y., Zhu X.-H., Rupprecht S., Lanagan M.T., Yang Q.X., Chen W. Значительное улучшение эффективности радиочастотной передачи и чувствительности приема для человека in vivo 31 P МРС-визуализация с использованием материалов со сверхвысокой диэлектрической проницаемостью при 7 T. Magn. Резон. Визуализация. 2017; 42:158–163. doi: 10.1016/j.mri.2017.07.019. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
33.
Byun J.-D., Seo J.-H., Kang T., Ryu Y., Kim K.-N. Катушка «птичья клетка» с индуктивно связанной решеткой РЧ-катушек для улучшения чувствительности |B 1 |-поля в 7-Тл МРТ. Дж. Магн. 2017;22:378–381. doi: 10.4283/JMAG.2017.22.3.378. [CrossRef] [Google Scholar]
34. Данг З.-М., Юань Дж.-К., Яо С.-Х., Ляо Р.-Дж. Гибкие нанодиэлектрические материалы с высокой диэлектрической проницаемостью для хранения энергии. Доп. Матер. 2013; 25:6334–6365. doi: 10.1002/adma.201301752. [PubMed] [CrossRef] [Академия Google]
35. Сео Дж.-Х., Хан С.-Д., Ким К.-Н. Улучшение интенсивности и однородности магнитного поля для МРТ мелких животных благодаря насадке из материала с высокой диэлектрической проницаемостью. Электрон. лат. 2016; 52: 898–900. doi: 10.1049/el.2016.0638. [CrossRef] [Google Scholar]
36. Эрнандес Д., Сео Дж.-Х., Ким К.-Н. Компоновка линейной решетки с использованием составных право-/левосторонних линий передачи для магнитно-резонансной томографии. Междунар.
Дж. Система обработки изображений. 2020;30:216–223. doi: 10.1002/ima.22349. [Перекрестная ссылка] [Академия Google]
37. Li Z., Willoquet G., Guillot G., Hosseinnezhadian S., Jourdain L., Poirier-quinot M., Darrasse L., Ginefri J.C. Исследование двух принципов бесконтактной настройки малых монолитных радиочастотных катушек МРТ. и разработка автоматизированной системы на основе пьезоэлектрического двигателя. Сенсор Привод A Физ. 2016; 241:176–189. doi: 10.1016/j.sna.2016.02.008. [CrossRef] [Google Scholar]
38. Caloz C., Itoh T., Rennings A. Метаматериал CRLH с утечкой волны и резонансные антенны. Антенна IEEE. Пропаг. Маг. 2008; 50: 25–39. doi: 10.1109/MAP.2008.4674709. [CrossRef] [Google Scholar]
39. Caloz C., Sanada A., Itoh T. Новый композитный направленный ответвитель со связанными правыми и левыми линиями с произвольным уровнем связи и широкой полосой пропускания. IEEE транс. Микров. Теория Тех. 2004; 52: 980–992. doi: 10.1109/TMTT.2004.823579. [CrossRef] [Google Scholar]
40.
Lai A., Itoh T., Caloz C. Композитные право/левосторонние метаматериалы для линий передачи. IEEE Микров. Маг. 2004; 5:34–50. doi: 10.1109/MMW.2004.1337766. [Перекрестная ссылка] [Академия Google]
41. Lee C.J., Huang W., Gummalla A., Achour M. Малые антенны на основе структур CRLH: концепция, конструкция и приложения. Антенна IEEE. Пропаг. Маг. 2011; 53:10–25. doi: 10.1109/MAP.2011.5949321. [CrossRef] [Google Scholar]
42. Puddu C., Rao M., Xu X., Deppe M.H., Collier G., Maunder A., Chan H.-F., Zanche N.D., Robb F., Wild J.M. Асимметричная РЧ-катушка в форме птичьей клетки для всего тела без РЧ-экрана для МРТ гиперполяризованных легких 129 Xe при 1,5 Тл. Резон. Мед. 2021; 86: 3373–3381. doi: 10.1002/mrm.28915. [PubMed] [CrossRef] [Google Scholar]
43. Ким К.-Н., Хан С.-Д., Сео Дж.-Х., Хо П., Ю Д., Им Г.Х., Ли Дж.Х. Асимметричная катушка в виде птичьей клетки для МРТ мелких животных при 7T. Магн. Резон. Мед. науч. 2017;16:253–258. doi: 10.2463/mrms.
tn.2016-0149. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
44. Seo J.-H., Ryu Y., Han S.-D., Song H., Kim H.-K., Kim K. .-Н. Влияние биологического объекта, экранирующей клетки и резонансной частоты на распространение радиоволн в катушке «птичья клетка». Электрон. лат. 2016; 52:801–803. дои: 10.1049/эл.2016.0533. [CrossRef] [Google Scholar]
45. Сео Дж.-Х., Сон Х., Ким Х.Дж., Хан С.-Д., Хо П., Ким Д., Рю Ю., Ким К.-Н. Матрица приемопередатчиков Гельмгольца для улучшения однородности поля |B 1 | при магнитно-резонансной томографии 7-T. физ. волна фен. 2017;25:147–150. doi: 10.3103/S1541308X17020121. [CrossRef] [Google Scholar]
46. Seo J.-H., Han S.D., Kim K.N. Конструкция перекрещивающейся двухслойной катушки типа «птичья клетка» для улучшения однородности поля B 1 + для магнитно-резонансной томографии мелких животных на частоте 300 МГц. Дж. Магн. 2015;20:308–311. doi: 10.4283/JMAG.2015.20.3.308. [Перекрестная ссылка] [Академия Google]
47.
Welsch G.H., Mamisch T.C., Weber M., Horger W., Bohndorf K., Trattnig S. Морфологическая и биохимическая визуализация суставного хряща голеностопного сустава с высоким разрешением при 3,0 Тл с использованием новой специальной катушки с фазированной решеткой: Исследование воспроизводимости in vivo. Скелетный радиол. 2008; 37: 519–526. doi: 10.1007/s00256-008-0474-z. [PubMed] [CrossRef] [Google Scholar]
48. Zanche N.D., Chhina N., Teh K., Randell C., Pruessmann K.P., Wild J.M. Асимметричная квадратурная расщепленная катушка типа «птичья клетка» для гиперполяризованного 3 МРТ легких при 1,5 Тл. Магн. Резон. Мед. 2008; 60: 431–438. doi: 10.1002/mrm.21664. [PubMed] [CrossRef] [Google Scholar]
49. Ahmad S.F., Kim Y.C., Choi I.C., Kim H.D. Недавний прогресс в технологии радиочастотных катушек для птичьей клетки для системы МРТ. Диагностика. 2020;10:1017. doi: 10.3390/диагностика10121017. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
50. Labbé A. , Authelet G., Baudouy B., van der Beek C.J., Briatico J., Darrasse L., Poirier-Quinot M. Недавние достижения и проблемы в разработке радиочастотной катушки HTS для МРТ. Передний. физ. 2021;9:386. doi: 10.3389/fphy.2021.705438. [CrossRef] [Google Scholar]
51. Doty F.D., Entzminger G., Kulkarni J., Pamarthy K., Staab J.P. Технология радиочастотной катушки для МРТ мелких животных. ЯМР Биомед. 2007; 20: 304–325. doi: 10.1002/nbm.1149. [PubMed] [CrossRef] [Google Scholar]
52. David E.S., Guangping D., Matthias N., Bruce R.R., Ravi S. МРТ сердца у мышей при 9,4 тесла с передающей-приемной поверхностной катушкой и адаптированной для сердца алгоритм коррекции интенсивности. Дж. Магн. Резон. Визуализация. 2007;26:279–287. [PubMed] [Google Scholar]
53. Янс В., Дондорп В., Гуссенс Э., Мертес Х., Пеннингс Г., де Верт Г. Баланс благополучия животных и вспомогательной репродукции: этика доклинических исследований на животных для тестирования новых репродуктивные технологии. Мед. Философия здравоохранения. 2018;21:537–545. doi: 10.1007/s11019-018-9827-0. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
54. Пасупулети М.К., Молахаллы С.С., Салваджи С. Этические принципы, профиль животных, различные модели животных, используемые в исследованиях пародонта, с альтернативами и перспективами на будущее. Дж. Индийская соц. Пародонтол. 2016;20:360–368. дои: 10.4103/0972-124Х.186931. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
55. Варга О., Хансен А., Сандо П., Олссон И. Валидация моделей животных для доклинических исследований: научная и этическая дискуссия. АТЛА Альтерн. лаборатория Аним. 2010; 38: 245–248. doi: 10.1177/026119291003800309. [PubMed] [CrossRef] [Google Scholar]
56. Champagne C., Yoshinari N., Oetjen J.A., Riché E.L., Beck J.D., Offenbacher S. Гендерные различия в системном воспалении и образовании атером после Инфекция Porphyromonas gingivalis у гетерозиготных мышей с дефицитом аполипопротеина Е. J. Периодонтальная рез. 2009; 44: 569–577. doi: 10.1111/j.1600-0765.2008.01156.x. [PubMed] [CrossRef] [Google Scholar]
57. Брейвик Т., Гундерсен Ю., Джермо П., фон Хёрстен С., Опстад П.К. Активация никотиновых ацетилхолиновых рецепторов опосредует вызванное никотином усиление экспериментального периодонтита. J. Периодонтальная рез. 2009;44:110–116. doi: 10.1111/j.1600-0765.2008.01095.x. [PubMed] [CrossRef] [Академия Google]
58. Перейра С., Вирарагхаван П., Гош С., Ганди М. Эксперименты на животных и этика в Индии: CPCSEA имеет значение. Альтерн. лаборатория Аним. 2004; 32: 411–415. doi: 10.1177/0261192
201s67. [PubMed] [CrossRef] [Google Scholar]59. Ричмонд Дж. Уточнение, сокращение и замена использования животных для нормативных испытаний: будущие улучшения и внедрение в рамках нормативной базы. ИЛАР Дж. 2002; 43: S63–S68. doi: 10.1093/ilar.43.Suppl_1.S63. [PubMed] [CrossRef] [Академия Google]
60. Eising E.G., Hughes J., Nolte F., Jentzen W., Bockisch A. Ожоговая травма с помощью ядерно-магнитно-резонансной томографии. клин. Визуализация. 2010; 34: 293–297. doi: 10.1016/j.clinimag.2009.06.025. [PubMed] [CrossRef] [Google Scholar]
61. Tian J., Shrivastava D., Strupp J., Zhang J., Vaughan J.T. От 7T до 10,5T: B 1 + , SAR и распределение температуры для МРТ головы и тела. проц. Междунар. соц. Магн. Резон. Мед. 2012;20:2666. [Google Scholar]
62. Эрьяман Ю., Акин Б., Аталар Э. Уменьшение радиочастотного нагрева имплантата за счет модификации электрического поля передающей катушки. Магн. Резон. Мед. 2011;65:1305–1313. doi: 10.1002/mrm.22724. [PubMed] [CrossRef] [Академия Google]
63. Фидлер Т.М., Лэдд М.Е., Битц А.К. Моделирование SAR и безопасность. НейроИзображение. 2018; 168:33–58. [PubMed] [Google Scholar]
64. Ниендорф Т., Граэссл А., Талхаммер К., Дирингер М.А., Краус О., Санторо Д., Фукс К., Хезель Ф., Вайцис С., Иттерманн Б., и другие. Прогресс и перспективы магнитного резонанса сердца человека в сверхвысоких полях: взгляд физики. Дж. Магн. Резон. 2013; 229:208–222. doi: 10.1016/j.jmr.2012.11.015. [PubMed] [CrossRef] [Google Scholar]
65. Гарсия М.М., Оливейра Т.Р., Папоти Д., Хаим К.Т., Отадуй М.К.Г., Эрни Д., Зилка В. Экспериментальные и численные исследования катушки малого животного для сверхвысоких полевая магнитно-резонансная томография (7T) Curr. Реж. Биомед. англ. 2019;5:525–528. doi: 10.1515/cdbme-2019-0132. [CrossRef] [Google Scholar]
66. Nitz W.R., Brinker G., Diehl D., Frese G. Удельная скорость поглощения как плохой показатель нагрева имплантата, связанного с магнитным резонансом. Вкладывать деньги. Радиол. 2005; 40: 773–776. doi: 10.1097/01.rli.0000185898.59140.91. [PubMed] [CrossRef] [Google Scholar]
67. Nakamura T., Fukuda K., Hayakawa K., Aoki I., Matsumoto K., Sekine T., Ueda H., Shimizu Y. Механизм ожоговой травмы при магнитно-резонансная томография (МРТ). Простые петли могут вызвать тепловое поражение. Передний. Мед. биол. англ. 2001; 11: 117–129.. [PubMed] [Google Scholar]
68. Chen B., Wang J., Qi H., Zhang J., Chen S., Wang X. Удельная скорость поглощения тканями крыс при воздействии электромагнитных плоских волн на частоте диапазоне 0,05–5 ГГц и SARwb у свободноподвижных крыс. Австралия. физ. англ. науч. Мед. 2017;40:21–28. doi: 10.1007/s13246-017-0522-x. [PubMed] [CrossRef] [Google Scholar]
69. Йи К.С. Численное решение начально-краевых задач для уравнений Максвелла в изотропных средах. IEEE транс. Антенны Распространение. 1996;14:302–307. [Google Scholar]
70. Холт Д.И. Принцип взаимности в расчетах уровня сигнала — математическое руководство. Концепции Маг. Резон. 2000; 12: 173–187. doi: 10.1002/1099-0534(2000)12:4<173::AID-CMR1>3.0.CO;2-Q. [CrossRef] [Google Scholar]
71. Im G.H., Seo J.-H., Kim K.-N., Heo P., Chung C.C., Jang M.S., Lee J.H., Kim S.I. /радиочастотная катушка только для приема для улучшения однородности B 1 при 7 Тл. J. Корейская физ. соц. 2014; 65: 616–624. дои: 10.3938/jkps.65.616. [CrossRef] [Google Scholar]
72. Кагадис Г.К., Форд Н.Р., Карнабатидис Д.Н., Лудос Г.К. Справочник по визуализации мелких животных: доклиническая визуализация, терапия и применение. CRC Press, Taylor & Francis Group; Нью-Йорк, штат Нью-Йорк, США: 2016. стр. 438–441. [Google Scholar]
73. Грубер Б., Фрелинг М., Лейнер Т., Кломп Д.В.Дж. ВЧ-катушки: Практическое руководство для нефизиков. Дж. Магн. Резон. Визуализация. 2018; 48: 590–604. doi: 10.1002/jmri.26187. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
74. Haase A., Odoj F., Von Kienlin M., Warnking J., Fidler F., Weisser A., Nittka M., Rommel E., Lanz T., Kalusche B., et al. ЯМР-зонды для приложений in vivo. Концепции Маг. Резон. 2000; 12: 361–388. doi: 10.1002/1099-0534(2000)12:6<361::AID-CMR1>3.0.CO;2-L. [CrossRef] [Google Scholar]
75. Delgado P.R., Kuehne A., Periquito J.S., Millward J.M., Pohlmann A., Waiczies S., Niendorf T. B 1 коррекция неоднородности RARE MRI с приемными поверхностными радиочастотными датчиками. Магн. Резон. Мед. 2020; 84: 2684–2701. doi: 10.1002/mrm.28307. [PubMed] [CrossRef] [Академия Google]
76. Вайдья М.В., Коллинз С.М., Содиксон Д.К., Браун Р., Виггинс Г.К., Латтанзи Р. Зависимость B 1 + и B 1 − полей от электрических свойств поверхностных катушек образца и рабочей частоты МР. Концепции Маг. Резон. Часть B Magn. Резон. англ. 2016;46:25–40. doi: 10.1002/cmr.b.21319. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
77. Склинда К., Карпович Ю., Степневский А. Электромагнитное облучение персонала, участвующего в МРТ-исследованиях сердца, на томографах 1,5Тл, 3Тл и 7Тл. Междунар. Дж. Окружающая среда. Рез. Здравоохранение. 2022;19:76. doi: 10.3390/ijerph2
76. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
78. Seo J.-H., Chung J.-Y. Предварительное исследование эталонной РЧ-катушки на МРТ 11,7 Тл: основано на моделировании электромагнитного поля гибридной РЧ-катушки в зависимости от диаметра и длины при 3,0, 7,0 и 11,7 Тл. Датчики. 2022;22:1512. doi: 10.3390/s22041512. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
79. Seo J.-H., Han S.D., Kim K.-N. Исследование распределения поля B 1 и выделения ВЧ мощности в катушке типа «птичья клетка» в зависимости от количества ветвей катушки при 4,7 Тл, 7,0 Тл и 11,7 Тл. J. Korean Phys. соц. 2015; 66: 1822–1826. дои: 10.3938/jkps.66.1822. [CrossRef] [Google Scholar]
80. Cao Z., Park J., Cho Z.-H., Collins C.M. Численная оценка однородности изображения, отношения сигнал-шум и удельной скорости поглощения для изображений головного мозга человека при 1,5, 3, 7, 10,5 и 14T в 8-канальном массиве передачи/приема. Дж. Магн. Резон. Визуализация. 2015;41:1432–1439. doi: 10.1002/jmri.24689. [Статья PMC бесплатно] [PubMed] [CrossRef] [Google Scholar]
81. Карбоне Л. Оценка использования мышей и крыс в американских лабораториях путем экстраполяции видов, регулируемых Законом о защите животных. науч. 2021;11:493. doi: 10.1038/s41598-020-79961-0. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
82. Sinmez C.C., Yasar A. Использование экспериментальных животных в Турции: сравнение с другими странами. Альтерн. лаборатория Аним. 2019;47:82–92. doi: 10.1177/0261192919861874. [PubMed] [CrossRef] [Google Scholar]
83. Lee S.Y., Lee D.Y., Kang J.H., Jeong J.W., Kim J.H., Kim H.W., Oh D.H., Kim J.-M., Rhim S.-J., Kim Г.-Д. и др. Альтернативные экспериментальные подходы к сокращению использования животных в биомедицинских исследованиях. Дж. Друг Делив. науч. Технол. 2022;68:103131. doi: 10.1016/j.jddst.2022.103131. [Перекрестная ссылка] [Академия Google] 9
М. Луа, Д. Ванб, Л.-П. Wangc’*, X.-D. Zhangd
a Факультет математических наук, Университет Цинхуа, Пекин, Китай b Факультет математики, Калифорнийский университет, Ирвин, Калифорния 92697-3875, США c Институт информационных технологий Китайской академии наук, Пекин, Китай d Кафедра математики и MOE—LSC, Шанхайский университет Цзяо Тонг, Шанхай, Китай
Информация о статье
Резюме
История статьи:
Поступила в редакцию 6 апреля 2013 г.
Получено в исправленном виде 23 января
Принято 25 января 2014 г. Доступно онлайн 25 февраля 2014 г. Сообщение Игоря Шпарлинского
MSC: 11L40 05C75 05C50
Новый алгебраический граф Кэли построен с использованием конечных полей. Он обеспечивает более гибкий источник графов-расширителей. Его связность, число компонент связности и граница диаметра изучаются с помощью оценки Вейля для сумм характеров. Кроме того, мы изучаем алгоритмическую задачу вычисления числа компонент связности и устанавливаем связь с проблемой целочисленной факторизации. 9Частично поддержан Программой 973 (2013CB834203) и Национальным фондом естественных наук Китая (гранты №№ 61373019, 61170289 и 11271256).
* Автор, ответственный за переписку.
Адреса электронной почты: [email protected] (М. Лу), [email protected] (Д. Ван), [email protected] (Л.-П. Ван) , [email protected] (X.-D. Zhang).
http://dx.doi.org/10.10167j.ffa.2014.01.014 1071-5797/© Elsevier Inc. , 2014. Все права защищены.
играет центральную роль в построении графов-расширителей. Случайно выбранный граф Кэли Cay(r,S) часто обладает хорошими свойствами с нетривиальной вероятностью. Однако детерминистически построить один такой хороший граф часто бывает сложнее. Обычно необходимо предположить дополнительную структуру группы r и ее подмножества S. Под алгебраическим графом Кэли мы подразумеваем, что r является мультипликативной группой конечного коммутативного кольца, а S c r является подмножеством с определенной алгебраической структурой, такой как ящик или интервал в каком-то смысле. Ящичная алгебраическая структура позволяет использовать мощные инструменты из теории чисел, чтобы условно доказать (при условии некоторой гипотезы Римана), что алгебраический граф Кэли Cay(r, S) действительно обладает желаемыми свойствами, если ящик достаточно велик. Таким образом, алгебраические графы Кэли представляют собой богатый источник графов-расширителей.
Важный пример приводит Чанг [1], который использует мультипликативную группу конечного расширения конечного поля и считает подмножество прямой в определенном смысле. Преимущество работы с конечным полем состоит в том, что иногда необходимую оценку можно доказать с помощью знаменитой границы Вейля для кривых над конечными полями. В этой статье мы вводим более общую конструкцию, используя мультипликативную группу конечного поля и беря в качестве подмножества те элементы, которые представлены определенными первичными полиномами. 9ß2 | ß2/ßi € Эд}.
Ясно, что Gd(n, q, а) — регулярный ориентированный граф порядка qn — 1 и его степень определяется выражением
д с | k
, где ¡i — функция Мёбиуса. Следует отметить, что граф Gd(n,q,a) зависит не только от d, n, q, но и от выбора a (т. е. от выбора неприводимого полинома f (x), который используется для представления поле расширения Fqn). В случае d = 1 Gi(n,q,a) сводится к графу Чанга из [1], который широко изучался (см. 9).0003
[2,4,5]). В этой статье мы изучаем общий d случай. Наше доказательство более прямое и использует оценку Вейля для сумм характеров.
Наш первый результат — следующая теорема. qd/2 + 1, то граф Gd(n, q, a) не всегда связен, так как ответ зависит от выбора a или неприводимого полинома f (x). Точнее имеем: 92d+2(|Pd|+1). Тогда существует хотя бы один a g Fgn степени n такой, что число компонент связности графа Gd(n,q,a) делится на (q — 1). В частности, Gd(n,q,a) не является связным хотя бы для одного элемента a степени n.
Как |Pd| — qd/d, оценка 2d + 2(|Pd| + 1) — 2qd/d является примерно квадратом оценки qd/2 в теореме 2. Это показывает, что условие в теореме 2 не слишком далеко от точности . Для оставшегося интервала, где
qd/2 + 1 < n < 2d + 2(|Pd| + 1) - 2qd/d, 9r51-1 )
Подробнее см. теорему 14 в разделе 2.
При случайно выбранном a граф Gd(n, q, a) связан с непренебрежимо малой вероятностью. Чтобы убедиться в этом, зафиксируем g G Pd как унитарный неприводимый. Тогда для случайно выбранного а элемент g(a) является первообразным корнем F*n с вероятностью
— 1) = n(_1_\
qn — 1 \loglog(qn — 1) J
, что равно непренебрежимо малым, где 0 — тотальная функция Эйлера. Таким образом, граф Gd(n, q, a) связан с непренебрежимо малой вероятностью. К сожалению, построение первообразного корня (или даже элемента высокого порядка) любого вида хорошо известная трудная проблема вычислительной теории чисел. В практическом применении трудность состоит в том, как быстро проверить, что данное Gd(n, q, a) является связным, и, в более общем смысле, как быстро вычислить количество его компонент связности, используя разреженный входной размер (n log q) O (1) графа Gd (n, q, a). В идеале мы хотели бы иметь детерминированный алгоритм со временем выполнения, ограниченным полиномом от (n log q) O ( 1), для вычисления числа компонент связности. В этом направлении имеем следующий условный результат.
Теорема 5. Предположим, что задана факторизация qn — 1. Затем можно вычислить количество компонент связности Gd(n,q,a) за время (n log q)O(1).
Было бы очень интересно удалить предположение о факторизации в приведенной выше теореме.
Важным типом графов является так называемый граф-расширитель, который возникает в вопросах проектирования сетей, соединяющих множество пользователей при использовании небольшого количества коммутаторов. Графы-расширители играют важную роль в информатике, математике и теории коммуникационных сетей. См. обзорную статью [3]. Регулярный граф степени k называется графом-расширителем, если модуль каждого нетривиального собственного значения графа много меньше тривиального собственного значения k. В последнем разделе мы показываем, что наш граф Gd(n, q, a) предоставляет новый источник графов-расширителей. 9qd/2 (1 — S). Тогда каждое нетривиальное собственное значение X оператора смежности графа Gd(n,q,a) удовлетворяет оценке
|X| < q-(1 — s) < |Pd|(1 — s) = xtriv(1 — s). d
В частности, граф Gd(n,q,a) является графом-расширителем.
Примечания. При построении графа Кэли Gd(n,q,a) мы взяли подмножество Ed в качестве множества всех унитарных первичных многочленов степени d. Также естественно взять подмножество множества всех унитарных неприводимых многочленов степени d или множества всех унитарных неприводимых многочленов, степень которых делит d. Результирующий граф асимптотически будет иметь аналогичные качества. Однако наш выбор подмножества в этой статье делает доказательства проще и чище, а результаты немного лучше. 9n/2
Количество элементов степени n в nnn. Число элементов, в которых находятся в собственном подполе, содержащем Fg, равно
deg(a) 1 = Kn — qn I < 2q Пусть H — подгруппа, порожденная g(a) для g G Пд. Ясно, что число компонент связности графа Gd(n, q, а) равно индексу [F*n : H]. Для делителя £ > 1 числа qn — 1 обозначим через He единственную подгруппу индекса £ в циклической группе F*n. Группа He состоит из £-й степени элементов из F*n. Обозначим через Id множество унитарных неприводимых полиномов g из Fq[x] таких, что deg(g) делит d. Каждый элемент из Pd является целочисленной степенью элемента из Id. Кроме того, |Ид| = |Pd|. Если а — элемент степени n в Fqn такой, что g(a) G He для всех g G Id, то H — подгруппа He и, следовательно, число компонент связности Gd (n, q, a) равно [F*n : H] = [F*n : He] [He : H] = £[Ht : H], который делится на £. Ne = |{a G Fqn: deg(a) = n, g(a) G He Vg G Id) |. Для доказательства теоремы достаточно доказать, что Ne > 0. Стандартное рассуждение суммы характеров показывает, что = EE n X (g(a)), xg = 1,g€ld deg(a)=n geId , где Xg обозначает характер F*n. В случае, когда xg 1 для всех g 6 Id, внутренняя сумма есть число nnn элементов степени n в Fgn. Во всех остальных (i 1 Id 1 — 1) случаях существует по крайней мере один g £ Id такой, что xg — нетривиальный характер. В таком случае стандартная оценка суммы характеров Вейля (см. следствие 2.3 в [5]) влечет 9(qd — 1)qn/2 = (qd + 1) qn/2, deg(a) , где мы использовали тот факт, что J2geId deg(g) есть число элементов в Fqd степени делит d и, таким образом, E deg(g) = qd. Сложив их вместе, мы заключаем, что /2 > qn — £lIdl(qd + 1)qn/2 > qn+d(qn-d — £}Id| + 1). Решение неравенства Приведенная выше теорема показывает, что граф Gd(n, q, a) не всегда связен. Это во многом зависит от выбора а. Интересный вопрос состоит в том, чтобы найти быстрый алгоритм, время выполнения которого ограничено полиномом от (n log q)O(1) для вычисления числа компонент связности. В этом направлении имеем следующий условный результат. Теорема 11. Предположим, что задана факторизация числа qn — 1. Затем можно вычислить количество компонент связности Gd(n,q,a) за время (n log q)O(1). 9кв/2 + 1; в противном случае Gd(n,q,a) уже связен. Пусть qn — 1 = pk1 ■■■Pkss, Hi = eF*n}. Hj — максимальные подгруппы F*n. Граф Gd(n, q, a) несвязен тогда и только тогда, когда подгруппа H = (g(a) | g£Pd) содержится в Hi для некоторого i. Это верно тогда и только тогда, когда g(a)(qn-1)/Pi = 1, Vg G Pd. Элементы Pd могут быть перечислены за время qd(n log q)O(1). Заметим, что max{s, (k1 +—-+ ks),qd} < n2 logq. Отсюда следует, что можно проверить, существует ли 1 ^ i ^ s такое, что H C Hi за время 9s такое, что H C Hij за время sqd(n log q)O(1) = (n log q)O(1). Продолжая в том же духе, в конце концов находим, что H = Hi1i2…iu, и, таким образом, число компонент связности равно [rf : H] = pi1 •• • piu. Общее необходимое время ограничено (k1 + • • • + ks)qd (n log q)O(1) = (n log q)O(1). □ Следствие 12. Число компонент связности Gd(n,q,a), являющееся индексом [rf : H], может быть вычислено за время O(qn/4). Доказательство. С помощью хорошо известного алгоритма решеточной факторизации LLL qn — 1 можно разложить на множители за время O(qn/4). □ Следствие 13. Если n четно, количество компонент связности Gd(n,q,a) можно вычислить за времени O(qn/8). Доказательство. qn — 1 = (qn/2 — 1)(qn/2 + 1) можно разложить на множители за время O(qn/8). □ Пусть Nd(n, q, a) обозначает количество компонент связности графа Gd(n, q, a). Интересная проблема состоит в том, чтобы дать хорошую общую оценку сверху для Nd(n,q,a), равномерную по a. В этом направлении у нас есть следующая простая грубая верхняя оценка. Теорема 14. 9Ex-1(ft) Emx(g(a))) . q q x=i KgePd y Применяя оценку Вейля из леммы 7, получаем, что Для того чтобы Mk (ft) > 0 для всех ft, достаточно иметь неравенство т. е. Это выполняется, если 2п > (п — 1)2к. = 2n + 4n log(n — 1) d — 2logg (n — 1) d d log q — 2log(n — 1) Теорема доказана. Для правильного делителя d числа n мы теперь проведем сравнение между графом Чанга Gi(n,qd,ft) и нашей более общей конструкцией Gd(n,q,a), где ft — корень неприводимого многочлена степени n/d в Fgd [x] и a — корень неприводимого многочлена степени n в Fg [x]. Ясно, что оба графа имеют qn — 1 вершин. Предположим, что n < qd/2 + 1. В этом случае как G1(n ,qd, ft), так и Gd(n,q,a) связны, и их границы диаметра n 4n log(n — 1) D < 2— + 1+__d d_' 9d dlogq - 2log(n - 1): n 4n log(n — 1) D < 2— + 1+__d v_' d d log q — 2log(n — 1) сравнимы. Но Gi(n,qd,a) qd-регулярна, а Gd(n,q,a) |Pd|-регулярна, где |Pd| ~ д < дд. Вычислительный вопрос состоит в том, чтобы запросить быстрый алгоритм со временем выполнения, ограниченным O(n log q)O(1), для вычисления диаметра D графа Gd(n,q,a). Ожидается, что это будет очень сложная проблема. Даже предполагая факторизацию qn = 1, мы все еще не знаем быстрого алгоритма для вычисления диаметра. Мы считаем, что вычисление диаметра связано с проблемой дискретного логарифмирования и проблемой суммы подмножества, обе из которых являются сложными задачами, используемыми в криптографии. 4. Графики-расширители 9y — ребро Gd(n, q, a). Если h(x) = x(x) — мультипликативный характер rf, то проверяют, что M(X)(x) = E X(xg(a)) = Xd(X)X(x), gePd Ad(x)=E X(g(a)). Это показывает, что каждый символ x является собственным вектором оператора M. По лемме Артина множество символов на rf C-линейно независимо. Так как число характеров равно qn — 1, то CFf имеет базис, состоящий из собственных векторов x матрицы M, где x проходит через все характеры rf. |X| < (1 - S) < |Pd|(1 - S) = Xtriv(1 - S). d В частности, граф Gd(n,q,a) является графом-расширителем. Заметим, что количество компонент связности Gd(n,q,a) равно кратности тривиального собственного значения |Pd| матрицы смежности M . Если использовать матрицу M и линейную алгебру напрямую для вычисления количества компонент связности, то время выполнения будет O (qn) O (1), что полностью экспоненциально в терминах n log q. Этот тривиальный алгоритм намного медленнее, чем условный результат в теореме 5.9(г)х(г(а)). Это показывает, что каждый характер x является собственным вектором оператора M *. Если x — характер, тривиальный на подгруппе, порожденной H = (g(a) | g e Pd) оператора rf, то собственное значение Sd (x) = E A(g) = qd , что является тривиальным собственным значением Xtriv = qd. Пусть n +2. Это действительно так для d = 1, как показали Кац [4] и Коэн [2]. Если x — характер, тривиальный на подгруппе, порожденной H = (g(a) | g£Pd) функции rf, то собственное значение 9qd/2(1 — S). Тогда каждое нетривиальное собственное значение X оператора смежности M для графа Gd(n.q.a) удовлетворяет оценке
