Внутренняя норма рентабельности инвестиционного проекта: Внутренняя норма доходности (ВНД) — что такое и как рассчитать — Кинотеатр "Художественный" кино, афиша, киноафиша, анонс, рейтинг, новость, кинотеатр, кинотеатры Москвы, кинофильм, прокат, лучший, Россия, Москва, кинотеатр Художественный

Содержание

Внутренняя норма доходности на excel

В данной статье мы рассмотрим, что такое внутренняя норма доходности, какой экономический смысл она имеет, как и по какой формуле рассчитать внутреннюю норму доходности, рассмотрим некоторые примеры расчёта, в том числе при помощи формул MS Exel.

Загрузить программу ВІ

Демонстрации решений

Что такое внутренняя норма доходности?

Внутренняя норма доходности (IRR — Internal Rate of Return) — один из основных критериев оценки инвестиционных проектов (доходности единицы вложенного капитала): ставка дисконта, при которой выполняется равенство суммы дисконтированных доходов по проекту (положительного денежного потока) дисконтированной сумме инвестиций (отрицательному денежному потоку, приведенному объему инвестиций), т.е. когда чистая текущая стоимость (NPV) равна нулю.

В финансово-экономической литературе довольно часто можно встретить синонимы внутренней ставки доходности:

внутренняя ставка доходности;
внутренняя ставка отдачи;
внутренняя норма прибыли;
внутренняя норма рентабельности;
внутренняя норма возврата инвестиций.

Внутренняя норма доходности отражает как отдачу инвестированного капитала в целом, так и отдачу первоначальных инвестиций. IRR – это ставка дисконтирования, которая приравнивает сумму приведенных доходов от инвестиционного проекта к величине инвестиций, т.е. вложения окупаются, но не приносят прибыль.

Таким образом, анализ внутренней нормы доходности (прибыли) отвечает на главный вопрос инвестора: насколько ожидаемый от проекта денежный поток оправдает затраты на инвестиции в этот проект. Поэтому инвестор при оценке проектов осуществляет расчет IRR каждого проекта и сравнивает его с требуемой нормой прибыли (рентабельности), т.е. со стоимостью своего капитала.

Этот расчет обычно ведется методом проб и ошибок, путем последовательного применения к чистому денежному потоку приведенных стоимостей при различных ставках процента. Главное правило: если внутренняя норма доходности меньше требуемой инвестору ставки дохода на вложенный капитал — проект отвергается, если больше — может быть принят.

Формула расчёта внутренней нормы доходности

Внутренняя норма доходности рассчитывается по следующей формуле:

где
NPV_IRR (Net Present Value) — чистая текущая стоимость, рассчитанная по ставке IRR;
CF_t (Cash Flow) – денежный поток в период времени t;
IC (Invest Capital) – инвестиционные затраты на проект в первоначальном периоде (тоже являются денежным потоком CF₀ = IC).
t – период времени.

или же данную формулу можно представить в виде:

Практическое применение внутренней нормы доходности

Внутренняя норма доходности применяется для оценки инвестиционной привлекательности проекта или для сопоставительного анализа с другими проектами. Для этого IRR сравнивают с эффективной ставкой дисконтирования, то есть с требуемым уровнем доходности проекта (r). За такой уровень на практике зачастую используют средневзвешенную стоимость капитала (Weight Average Cost of Capital, WACC).

Значение IRR	Комментарии
IRR>WACC	У инвестиционного проекта внутренняя норма доходности выше чем затраты на собственный и заемный капитал, т.е. данный проект имеет инвестиционную привлекательность
IRR	Инвестиционный проект имеет внутреннюю норму доходности ниже чем затраты на капитал, это свидетельствует о нецелесообразности вложения в него
IRR=WACC	Внутренняя норма доходность проекта равна средневзвешенной стоимости капитала, т. е. данный проект находится на минимально допустимом уровне доходности, поэтому следует произвести корректировки движения денежных средств и увеличить денежные потоки
IRR1>IRR2	Инвестиционный проект №1 имеет больший потенциал для вложения чем проект №2

Следует отметить, что вместо критерия сравнения WACC может быть использована любая другая норма доходности, например, ставка доходности по государственным облигациям, ставка по банковскому депозиту и т.п. Так, если процентная ставка по депозиту составляет 17%, а IRR инвестиционного проекта составляет 22%, то, очевидно, что деньги следует вкладывать в инвестиционный проект, а не размещать на депозит в банк.

Графический метод поиска внутренней ставки доходности

Предположим, что мы собираемся инвестировать 10 тыс. денежных единиц, и у нас есть варианты их инвестирования в 3 проекта каждый из которых, как предполагается, будет формировать определённые денежные потоки на протяжении 5 лет.

Период, лет	Проект №1	Проект №2	Проект №3
0	-10000	-10000	-10000
1	1000	1000	4000
2	4 000	1500	3000
3	2000	3000	2000
4	4000	4000	1000
5	2000	3000	1000

Продисконтируем вышеуказанные денежные потоки по 3-м проектам по разным процентным ставкам (от 0 до 14%) и на основе полученных результатов построим график.

На графике прослеживается чёткая взаимосвязь между ставкой дисконтирования и чистой текущей стоимостью: чем выше ставка дисконтирования, тем ниже дисконтированная стоимость.

Внутренняя норма доходности, как это следует из определения указанного в начале данной статьи, — это тот уровень ставки дисконта, при которой NPV=0. В нашем примере внутренняя норма доходности определяется в точках пересечения кривых с осью Х. В частности, для проекта №1 IRR составляет 8,9%, для проекта №2 IRR=6,6% и для проекта №3 IRR=4,4%.

Расчёт внутренней нормы доходности (IRR) при помощи MS Exel

Внутреннюю норму доходности можно довольно легко рассчитать при помощи встроенной финансовой функции ВСД (IRR) в MS Exel.

Функция ВСД возвращает внутреннюю ставку доходности для ряда потоков денежных средств, представленных их численными значениями. Эти денежные потоки не обязательно должны быть равными по величине (как в случае аннуитета), однако они должны иметь место через равные промежутки времени, например ежемесячно или ежегодно. При этом в структуре денежных потоков должен обязательно быть хотя бы один отрицательный денежный поток (первоначальные инвестиции) и один положительный денежный поток (чистый доход от инвестиции).

Также для корректного расчёта внутренней нормы доходности при помощи функции ВСД важен порядок денежных потоков, т.е. если потоки денежных средств отличаются по размеру в разные периоды, то их обязательно необходимо указывать в правильной последовательности.

Синтаксис функции ВСД:

ВСД(Значения;Предположение)

где
Значения — это массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности, учитывая требования указанные выше;
Предположение — это величина, о которой предполагается, что она близка к результату ВСД:

Microsoft Excel использует метод итераций для вычисления ВСД. Начиная со значения Предположение, функция ВСД выполняет циклические вычисления, пока не получит результат с точностью 0,00001 процента. Если функция ВСД не может получить результат после 20 попыток, то выдается значение ошибки #ЧИСЛО!.
В большинстве случаев нет необходимости задавать Предположение для вычислений с помощью функции ВСД. Если Предположение опущено, то оно полагается равным 0,1 (10 процентов).
Если ВСД возвращает значение ошибки #ЧИСЛО! или если результат далек от ожидаемого, можно попытаться выполнить вычисления еще раз с другим значением аргумента Предположение.

Пример расчёта внутренней ставки доходности (на основе данных о денежных потоках по трём проектам, которые рассматривались выше):

В частности для проекта №1 значение IRR=8,9%.

Расчёт внутренней нормы доходности в MS Exel при неравных промежутках времени для денежных потоков

Посредством Exel-функции ВСД можно довольно легко определить внутреннюю норму доходности, однако данную функцию можно применять лишь в том случае, если денежные потоки поступают с регулярной периодичностью (например, ежегодно, ежеквартально, ежемесячно). Однако на практике довольно часто возникают ситуации, когда денежные потоки поступают в разные временные промежутки. В таких случаях можно воспользоваться другой встроенной финансовой функцией Exel — ЧИСТВНДОХ, которая возвращает внутреннюю ставку доходности для графика денежных потоков, которые не обязательно носят периодический характер.

Синтаксис функции ЧИСТВНДОХ

ЧИСТВНДОХ(значения;даты;предположение)

где
Значения — ряд денежных потоков, соответствующий графику платежей, приведенному в аргументе Даты. Первый платеж является необязательным и соответствует затратам или выплате в начале инвестиции. Если первое значение является затратами или выплатой, оно должно быть отрицательным. Все последующие выплаты дисконтируются на основе 365-дневного года. Ряд значений должен содержать по крайней мере одно положительное и одно отрицательное значение.
Даты — расписание дат платежей, которое соответствует ряду денежных потоков. Даты могут идти в произвольном порядке.
Предположение — величина, предположительно близкая к результату ЧИСТВНДОХ.

Пример расчёта:

Модифицированная внутренняя норма доходности (MIRR)

Модифицированная внутренняя норма доходности (Modified Internal Rate of Return, MIRR) – показатель, который отражает минимальный внутренний уровень доходности проекта при осуществлении реинвестиций в проект. Данный проект использует процентные ставки, полученные от реинвестирования капитала.

Формула расчета модифицированной внутренней нормы доходности:

где
MIRR – внутренняя норма доходности инвестиционного проекта;
COF_t – отток денежных средств в периоды времени t;
CIF_t – приток денежных средств;
r – ставка дисконтирования, которая может рассчитываться как средневзвешенная стоимость капитала WACC;
d – процентная ставка реинвестирования капитала;
n – количество временных периодов.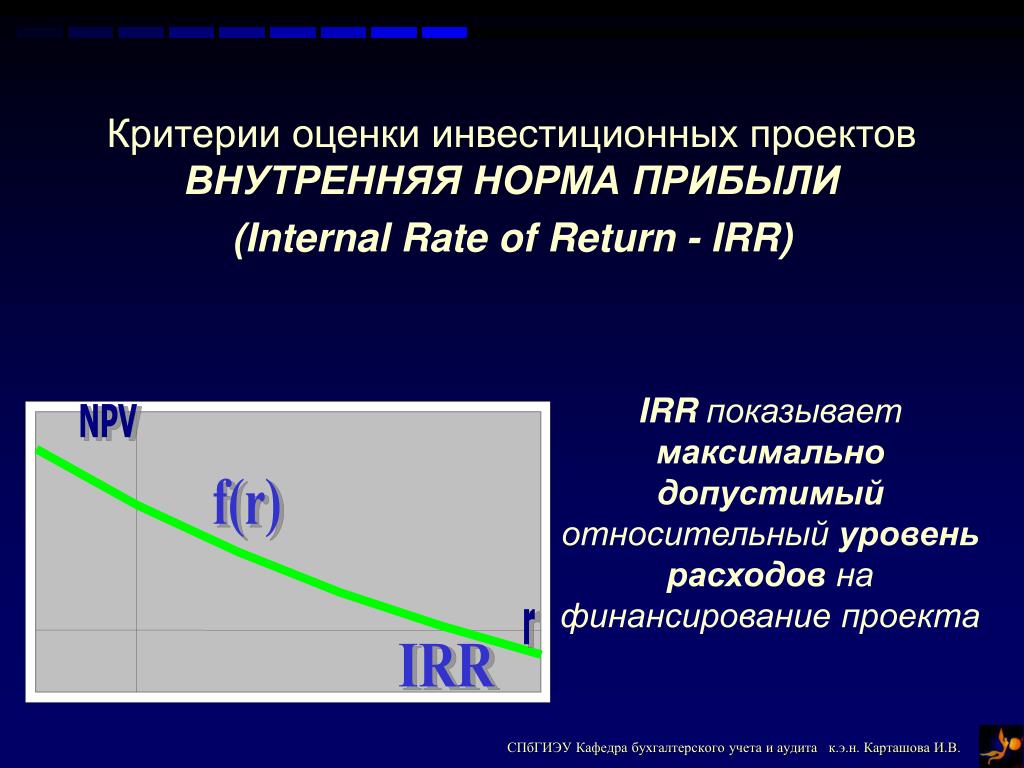

В MS Exel есть специальная встроенная финансовая функция МВСД для расчёта модифицированной внутренней ставки доходности.

Синтаксис функции МВСД:

МВСД(значения;ставка_финанс;ставка_реинвест)

где
Значения — массив или ссылка на ячейки, содержащие числовые величины. Эти числа представляют ряд денежных выплат (отрицательные значения) и поступлений (положительные значения), происходящих в регулярные периоды времени.
Ставка_финанс — ставка процента, выплачиваемого за деньги, используемые в денежных потоках.
Ставка_реинвест — ставка процента, получаемого на денежные потоки при их реинвестировании.

Преимущества и недостатки внутренней нормы доходности (IRR)

К основным преимуществам IRR можно отнести:

возможность сравнения различных инвестиционных проектов между собой с целью определения более привлекательных с точки зрения экономической эффективности использования имеющегося капитала. Сравнение может быть произведено и с неким условным эталоном, например, с процентной ставкой по депозитам;
возможность сравнения различных инвестиционных проектов с разным горизонтом инвестирования.

Основными недостатками показателя внутренней нормы доходности (IRR) являются:

сложность прогнозирования будущих денежных платежей. На размер планируемых платежей влияет множество факторов риска, влияние которые сложно объективно оценить;
невозможность определения абсолютных денежных средств от инвестирования;
при произвольном чередовании притоков и оттоков денежных средств в случае одного проекта могут существовать несколько значений IRR. Поэтому нельзя принять однозначное решение на основе показателя IRR;
показатель IRR не отражает размер реинвестирования в проект (данный недостаток решен в модифицированной внутренней норме доходности MIRR).

Почитать еще

Введение в финансовый анализ

Финансы – это язык любого бизнеса. К компетенции, необходимой для понимания и ведения бизнеса, относится

5 ключевых элементов финансового анализа

«Финансы», что с этим? Все дело в числах. Это мощная игра чисел, и понимание потенциала

Прогнозирование цен на акции и искусственный интеллект

Напомним, что прогнозирование цен на акции на самом деле является одной из самых сложных задач

Искусственный интеллект на финансовых рынках

Существует популярное представление о том, что искусственный интеллект может делать на финансовых рынках, и как

Большие данные для финансов

Сегодня одним из ключевых направлений для корпоративных лидеров становится работа с данными. Практически девять из

Семь шагов к успеху для прогнозной аналитики в финансовых услугах

Помните, когда вы начали свою карьеру и перспектива выхода на пенсию была событием в далеком

Анализ рисков

Принятие разумных, своевременных решений в финансовом планировании и аналитике (ФПиА) критически важно для вашего успеха.

Анализ акций

Анализ акций Предоставление высокоскоростных услуг со скоростью сообщений в миллионы в секунду поддерживает

Анализ финансового состояния предприятий

Аналитика финансовой деятельности Индустрия страхования обращается к аналитике, чтобы создать Алгоритмическое страхование как конкурентное преимущество.

Читайте о всех решениях

Какие бы задачи перед Вами не стояли, мы сможем предложить лучшие инструменты и решения

Смотреть

Несколько видео о наших продуктах

Инвестиционные процессы – интересная сфера бизнеса, в которой есть сторона, желающая выгодно вложить свои капиталы, и есть вторая сторона – которая «продает» свою бизнес идею и предпринимательские способности с целью получения доступа к финансам для реализации своих проектов. Это та сила, которая двигает экономику, промышленное и инновационное развитие.

Не существует абсолютно достоверного способа, чтобы определить, какой степенью привлекательности обладает тот или иной инвестиционный проект, риски невозврата инвестиций существуют всегда. Но есть ряд надежных индикаторов, которые могу значительно повысить вероятность успешного вложения капитала.

Внутренняя норма доходности (ВНД или IRR) – ключевой критерий анализа любого доступного для инвестирования проекта, который определяет минимальную норму дисконтирования, при которой дисконтированные доходы будут равны понесенным на приобретение актива или реализацию проекта расходам.

Использование метода внутренней нормы прибыли позволяет получить ответ об оправданности инвестиций в тот или иной проект и о том объеме инвестиций, которые минимально необходимы, чтоб проект как минимум вышел на самоокупаемость.

Корректно подобранная ставка дисконтирования должна быть ниже показателя внутренней нормы прибыли, тогда проект потенциально способен принести доход и стать рентабельным, в противном случае он не сможет привлечь финансирование.

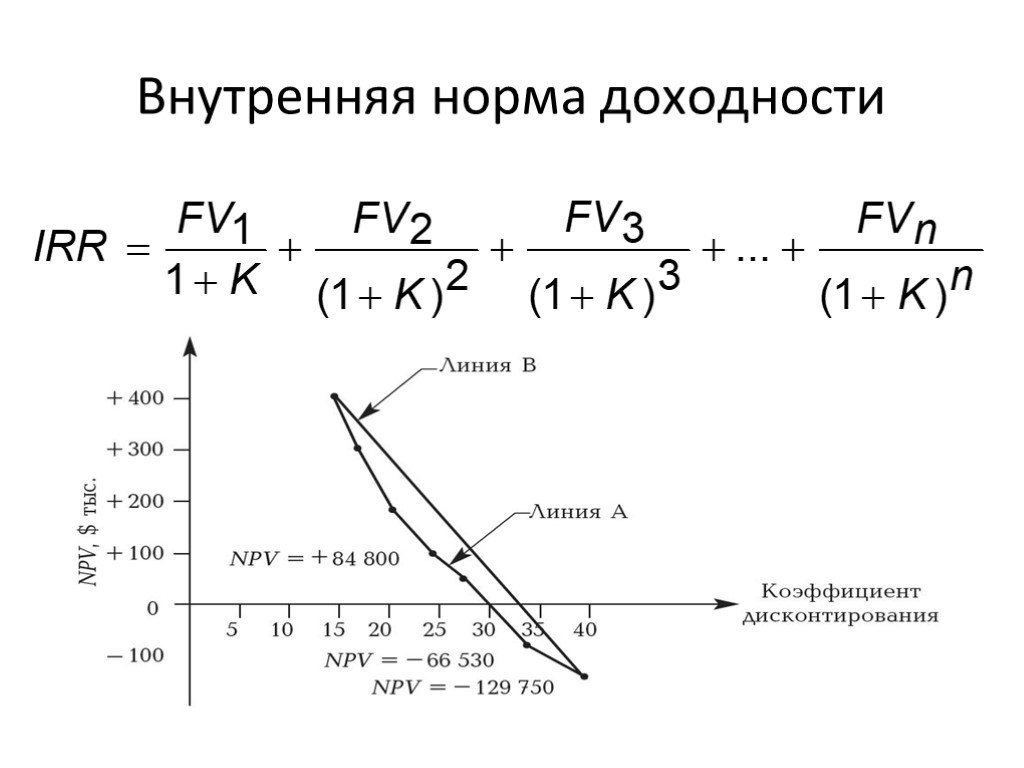
Чтобы проект соответствовал целям своего инициатора и был способен обеспечить привлекательность и высокий уровень рентабельности для потенциальных инвесторов, скачайте с нашего сайта полноценный готовый бизнес-план, включающий расчеты ключевых экономических и финансовых показателей. Также у вас есть отличная возможность заказать индивидуальный бизнес-план «под ключ», в котором будет раскрыто максимум важных для организации компании моментов ее становления и стратегического развития.

чистый дисконтированный доход или NPV (с англ. Net Present Value) – это общая величина всех финансовых потоков инвестиционного проекта, приведенная к единому показателю соотнесения доходов и расходов, распределенных во времени;
денежные или финансовые потоки CF (от англ. Cash Flows) – объем поступлений и оттоков денежных средств за определенный период реализации проекта (месяц, год и т. д.), учитывающий в том числе и текущие инвестиционные вливания. Первая инвестиционная сумма, вложенная в начале проекта, естественно учитывается, как финансовый поток с отрицательным значением.
ставка дисконтирования R – это процентное соотношение, которое описывает изменение стоимости денежных средств в течение срока реализации проекта и приводит их реальную ценность к текущему состоянию и времени. Если говорить проще – то это стоимость или процент за использование заемного или инвестиционного капитала.
средневзвешенная стоимость капитала WACC (от англ. Weighted Average Cost of Capital) – если в проект привлекается несколько источников финансирования, то в качестве нормы дисконтирования используется средняя ставка по всем источникам.

Внутренняя норма прибыли применяется как для оценки индивидуальной привлекательности инвестиционного проекта, так и для того, чтобы сравнить и сделать выбор при наличии нескольких альтернативных бизнес планов или идей.

Чтобы осуществить это на практике, рассчитанное значение внутренней нормы прибыли сравнивают с эффективной ставкой дисконтирования, которая по сути является требуемой ставкой рентабельности. При этом такой требуемой ставкой часто выступает показатель средневзвешенной стоимости капитала (WACC).

IRR равна WACC: в подобной ситуации проект выйдет на точку окупаемости, и инвестор сможет лишь вернуть свои вложения, без какой-либо прибыли и рентабельности. То есть следует корректировать проект и выводить его в плоскость ситуации №1.

WACC – это не истина в последней инстанции. На практике широко используются следующие нормативные показатели: доходность государственных ценных бумаг, средние ставки по банковским вкладам и депозитам и т.д. И тогда, полученное значение внутренней нормы прибыли должно быть выше этого нормативного показателя (если есть вариант положить деньги в банк под 12% или вложить их в инвестиционный проект под 13%, то естественно второй вариант выгоднее для инвестора).

предоставляет инструмент сравнения предпочтительности инвестиций по эффективности применения капитала. Если у двух проектов одинаковые NPV и ставки дисконта, то предпочтительнее будет тот, который покажет большее значение рентабельности с рубля вложенных средств;
позволяет сравнивать проекты с отличающимися горизонтами планирования, то есть когда проекты предполагают различную длительность их исполнения и инвестирования. Предпочтительнее будет тот бизнес план, для которого значение величины чистого дисконтированного дохода выше в долгосрочной перспективе.

сложность и неоднозначность прогнозирования финансовых потоков, что связано с невозможностью предсказать точно, какой доход будет итогом определенного периода реализации проекта. На прибыль влияет огромное количество внешних и внутренних факторов, и предсказать поведение их всех представляется невыполнимой задачей;

Если планируете начать бизнес, например, в сфере переработки мусора и отходов, то типовой бизнес-план будет вам полезен. Вы сможете запланировать доходы, расходы, налоги, рассчитать прибыль, рентабельность и другие важные финансовые и инвестиционные показатели.

Если говорить в общем, то грамотное использование метода расчета внутренней доходности, позволит произвести достаточно объективную оценку привлекательности проекта с точки зрения инвестиций в него или выбрать лучшую из нескольких аналогичных бизнес идей.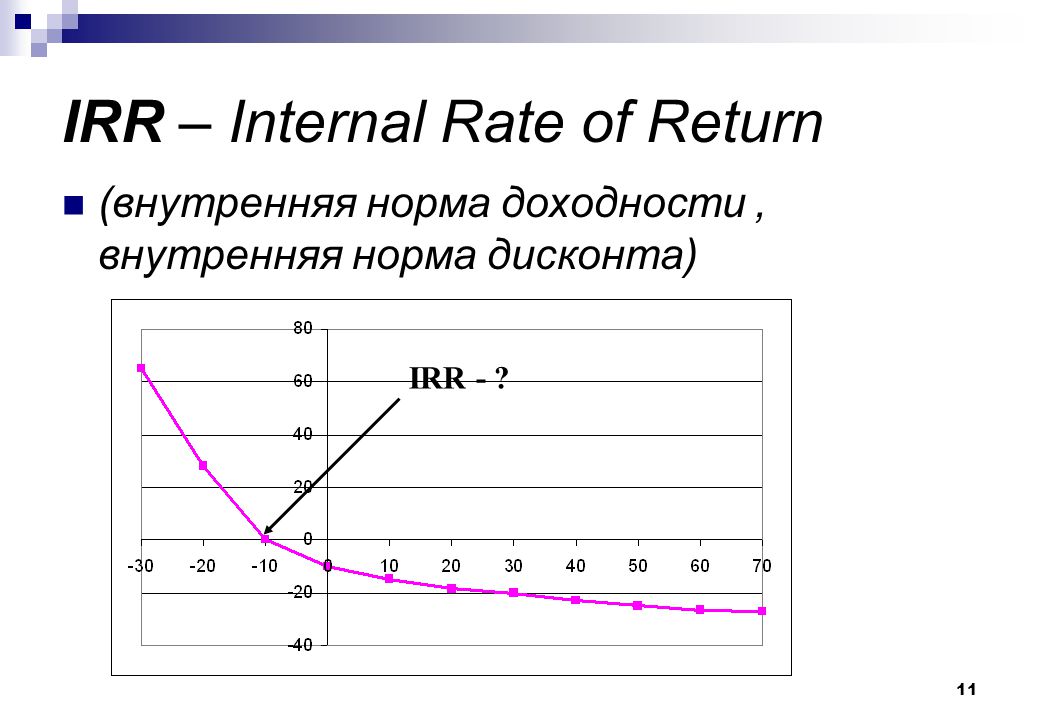 Чтобы обеспечить корректное и грамотное проектирование, скачайте у нас на сайте полноценный структурированный бизнес-план, с расчетами финансовых и экономических показателей инвестиционной привлекательности бизнеса. Тогда вы ускорите процессы привлечения инвестиций и приблизите период получения первой прибыли новой компании. Также вы можете заказать индивидуальный бизнес-план «под ключ», в котором учитывается большинство специфических моментов создания и развития конкретной компании или предприятия.

Чистая приведенная стоимость (NPV) представляет собой разницу между приведенной стоимостью притока денежных средств и приведенной стоимостью оттока денежных средств за определенный период времени. NPV используется при составлении бюджета капиталовложений и инвестиционном планировании для анализа рентабельности планируемых инвестиций или проекта.

NPV является результатом расчетов, которые определяют текущую стоимость будущего потока платежей с использованием надлежащей ставки дисконтирования. Как правило, проекты с положительной NPV стоят того, чтобы их брать, а проекты с отрицательной NPV — нет.

Если чистая приведенная стоимость проекта или инвестиции положительна, это означает, что его норма прибыли будет выше ставки дисконтирования. 9t} — \text{первоначальные инвестиции} \\ &\textbf{где:}\\ &i=\text{Требуемая доходность или ставка дисконтирования}\\ &t=\text{Количество периодов времени}\\ \end{выровнено} NPV = (1 + i) tДенежный поток – первоначальные инвестиции, где: i = требуемая доходность или коэффициент дисконтирования, t=количество периодов времени
Если анализировать долгосрочный проект с несколькими денежными потоками, то формула для NPV проекта выглядит следующим образом:
Н п В «=» ∑ т «=» 0 н р т ( 1 + я ) т где: р т «=» чистый приток-отток денежных средств за один период т я «=» ставка дисконтирования или доход, который можно было бы получить при альтернативных инвестициях т «=» количество периодов времени \begin{align} &NPV = \sum_{t = 0}^n \frac{R_t}{(1 + i)^t}\\ &\textbf{где:}\\ &R_t=\text{чистый приток денежных средств- оттоки в течение одного периода }t\\ &i=\text{ставка дисконтирования или доход, который можно было бы получить при альтернативных инвестициях}\\ &t=\text{количество периодов времени}\\ \end{выровнено} NPV=t=0∑n(1+i)tRtгде:Rt=чистый приток-отток денежных средств в течение одного периода ti=ставка дисконтирования или доход, который можно получить в альтернативных инвестицияхt=количество периодов времени
Если вы не знакомы с нотацией суммирования, вот более простой способ запомнить концепцию NPV:
Н п В «=» Сегодняшнее значение ожидаемых денежных потоков − Сегодняшняя стоимость вложенных денежных средств NPV = \text{Сегодняшняя стоимость ожидаемых денежных потоков} — \text{Сегодняшняя стоимость вложенных денежных средств} NPV = сегодняшняя стоимость ожидаемых денежных потоков — сегодняшняя стоимость вложенных денежных средств.
Что NPV может рассказать вам
NPV учитывает временную стоимость денег и может использоваться для сравнения норм доходности различных проектов или для сравнения прогнозируемой нормы прибыли с пороговой нормой, необходимой для одобрения инвестиций. Временная стоимость денег представлена в формуле NPV ставкой дисконтирования, которая может быть пороговой ставкой для проекта, основанного на стоимости капитала компании. Независимо от того, как определена ставка дисконтирования, отрицательная чистая приведенная стоимость показывает, что ожидаемая норма прибыли не соответствует ей, а это означает, что проект не создаст ценности.
В контексте оценки корпоративных ценных бумаг расчет чистой приведенной стоимости часто называют анализом дисконтированных денежных потоков (DCF). Это метод, используемый Уорреном Баффетом для сравнения чистой приведенной стоимости будущих DCF компании с ее текущей ценой.
Ставка дисконтирования занимает центральное место в формуле. Это объясняет тот факт, что, пока процентные ставки положительны, доллар сегодня стоит больше, чем доллар в будущем. Инфляция со временем обесценивает деньги. Между тем, сегодняшний доллар можно инвестировать в безопасный актив, такой как государственные облигации; более рискованные инвестиции, чем Treasurys, должны обеспечивать более высокую норму прибыли. Как бы то ни было, ставка дисконтирования — это просто базовая норма прибыли, которую проект должен превысить, чтобы быть стоящим.
Например, инвестор может получить 100 долларов сегодня или через год. Большинство инвесторов не захотят откладывать получение $100 сегодня. Однако что, если бы инвестор мог выбрать: получить 100 долларов сегодня или 105 долларов через год? Норма прибыли 5 % могла бы иметь смысл, если бы сопоставимые инвестиции с равным риском предлагали меньше за тот же период.
Если, с другой стороны, инвестор мог бы заработать 8% без риска в течение следующего года, то предложение в размере 105 долларов в год было бы недостаточным. В этом случае 8% будет ставкой дисконтирования.
Положительная NPV и отрицательная NPV
Положительная чистая приведенная стоимость указывает на то, что прогнозируемая прибыль, полученная от проекта или инвестиции, дисконтированная по их текущей стоимости, превышает ожидаемые затраты, в том числе в сегодняшних долларах. Предполагается, что инвестиции с положительной NPV будут прибыльными.
Инвестиции с отрицательной NPV принесут чистый убыток. Эта концепция является основой правила чистой приведенной стоимости, согласно которому следует рассматривать только инвестиции с положительной чистой приведенной стоимостью.
NPV можно рассчитать с помощью таблиц, электронных таблиц (например, Excel) или финансовых калькуляторов.
Как рассчитать чистую приведенную стоимость с помощью Excel
В Excel есть функция NPV, которую можно использовать для простого расчета чистой приведенной стоимости ряда денежных потоков. Функция NPV в Excel — это просто NPV, и полное требование к формуле:
= NPV (ставка дисконтирования, будущий денежный поток) + первоначальные инвестиции
Пример NPV, Excel.
В приведенном выше примере формула, введенная в серую ячейку NPV, выглядит следующим образом:
= NPV (зеленая ячейка, желтые ячейки) + синяя ячейка
= NPV(C3, C6:C10) + C5
Пример расчета NPV
Представьте себе, что компания может инвестировать в оборудование, которое будет стоить 1 миллион долларов и, как ожидается, будет приносить доход в размере 25 000 долларов в месяц в течение пяти лет. В качестве альтернативы компания может инвестировать эти деньги в ценные бумаги с ожидаемой годовой доходностью 8%. Руководство рассматривает оборудование и ценные бумаги как сопоставимые инвестиционные риски.
Существует два ключевых шага для расчета чистой приведенной стоимости инвестиций в оборудование:
Шаг 1: NPV первоначальных инвестиций
Поскольку оборудование оплачивается авансом, это первый денежный поток, включенный в расчет. Нет необходимости учитывать прошедшее время, поэтому не нужно сбрасывать со счетов немедленные расходы в размере 1 миллиона долларов.
Этап 2: NPV будущих денежных потоков
Определите количество периодов (t): Ожидается, что оборудование будет генерировать ежемесячный денежный поток в течение пяти лет, что означает, что в расчет будет включено 60 периодов после умножение количества лет денежных потоков на количество месяцев в году. 9{\ гидроразрыва {1} {12}}) — 1 = 0,64 \% Периодическая ставка = ((1+0,08)121)−1=0,64%
Предположим, что ежемесячные денежные потоки зарабатываются в конце месяца, а первый платеж поступает ровно через месяц после покупки оборудования. Это будущий платеж, поэтому его необходимо скорректировать с учетом временной стоимости денег. Инвестор может легко выполнить этот расчет с помощью электронной таблицы или калькулятора. Чтобы проиллюстрировать концепцию, первые пять платежей показаны в таблице ниже.
Изображение Сабрины Цзян © Investopedia 2020 9{60}} NPV=-$1,000,000+∑t=160(1+0,0064)6025,00060
Эту формулу можно упростить до следующего расчета:
Н п В «=» − $ 1 , 000 , 000 + $ 1 , 242 , 322,82 «=» $ 242 , 322,82 NPV = -\$1 000 000 + \$1 242 322,82 = \$242 322,82 NPV = — 1 000 000 долларов США + 1 242 322,82 доллара США = 242 322,82 доллара США.
В этом случае ЧДД положительна; оборудование должно быть закуплено. Если бы приведенная стоимость этих денежных потоков была отрицательной из-за большей ставки дисконтирования или меньшего чистого денежного потока, то инвестиции не имели бы смысла.
Ограничения чистой приведенной стоимости
Заметным ограничением анализа NPV является то, что он делает предположения о будущих событиях, которые могут оказаться неверными. Используемое значение ставки дисконтирования является оценочным, в то время как стоимость инвестиций и их прогнозируемая доходность обязательно являются оценочными. Расчет NPV надежен настолько, насколько надежны лежащие в его основе допущения.
Формула NPV дает результат в долларах, который, хотя его легко интерпретировать, может не отражать всей картины. Рассмотрим следующие два варианта инвестирования: вариант А с чистой приведенной стоимостью 100 000 долларов или вариант Б с чистой приведенной стоимостью 1000 долларов.
Формула NPV
Плюсы
Учитывает временную стоимость денег
Включает дисконтированный денежный поток с использованием стоимости капитала компании
Возвращает одно значение в долларах, которое относительно легко интерпретировать
Может быть легко вычислить при использовании электронных таблиц или финансовых калькуляторов
Минусы
В значительной степени зависит от исходных данных, оценок и долгосрочных прогнозов
Не учитывает размер проекта или рентабельность инвестиций (ROI)
Может быть сложно рассчитать вручную, особенно для проектов с многолетним денежным потоком
Основан на количественных исходных данных и не учитывает нефинансовые показатели
NPV и период окупаемости
Легкий звонок, верно? Как насчет того, если вариант А требует первоначальных инвестиций в размере 1 миллиона долларов, а вариант Б обойдется всего в 10 долларов? Крайние числа в примере указывают на это. Формула NPV не оценивает окупаемость проекта (ROI), что является ключевым фактором для всех, у кого ограниченный капитал. Хотя формула NPV оценивает, какую ценность принесет проект, она не говорит вам, является ли это эффективным использованием ваших инвестиций.
Период окупаемости или метод окупаемости является более простой альтернативой NPV. Метод окупаемости рассчитывает, сколько времени потребуется, чтобы окупить инвестиции. Одним из недостатков этого метода является то, что он не учитывает временную стоимость денег. По этой причине периоды окупаемости, рассчитанные для долгосрочных инвестиций, имеют большую вероятность неточности.
Кроме того, при расчете периода окупаемости не учитывается, что произойдет после номинального возмещения инвестиционных затрат. Норма доходности инвестиций может значительно меняться с течением времени. Сравнение с использованием периодов окупаемости предполагает обратное.
NPV и внутренняя норма доходности (IRR)
Внутренняя норма доходности (IRR) рассчитывается путем решения формулы NPV для ставки дисконтирования, необходимой для того, чтобы сделать NPV равным нулю. Этот метод можно использовать для сравнения проектов разных временных отрезков на основе прогнозируемой доходности.
Например, IRR можно использовать для сравнения ожидаемой прибыльности трехлетнего проекта с доходностью 10-летнего проекта. Хотя IRR полезен для сравнения норм доходности, он может скрыть тот факт, что норма доходности трехлетнего проекта доступна только в течение трех лет и может не соответствовать после реинвестирования капитала.
Что означает чистая приведенная стоимость (NPV)?
Чистая приведенная стоимость (NPV) — это финансовый показатель, который стремится отразить общую стоимость инвестиционной возможности. Идея NPV состоит в том, чтобы спрогнозировать все будущие притоки и оттоки денежных средств, связанные с инвестициями, дисконтировать все эти будущие денежные потоки до сегодняшнего дня, а затем сложить их вместе. Полученное число после сложения всех положительных и отрицательных денежных потоков представляет собой чистую приведенную стоимость инвестиций. Положительная чистая приведенная стоимость означает, что после учета временной стоимости денег вы заработаете деньги, если продолжите инвестиции.
В чем разница между NPV и внутренней нормой доходности (IRR)?
NPV и внутренняя норма доходности (IRR) являются тесно связанными понятиями в том смысле, что IRR инвестиции представляет собой ставку дисконтирования, при которой чистая приведенная стоимость инвестиции равна нулю. Другой способ думать об этом состоит в том, что NPV и IRR пытаются ответить на два отдельных, но связанных между собой вопроса. Для NPV вопрос заключается в следующем: «Какова общая сумма денег, которую я заработаю, если продолжу эти инвестиции с учетом временной стоимости денег?» Для IRR вопрос заключается в следующем: «Если я продолжу эти инвестиции, какова будет эквивалентная годовая норма прибыли, которую я получу?»
Что такое хорошая чистая приведенная стоимость?
Теоретически чистая приведенная стоимость является «хорошей», если она больше нуля. В конце концов, расчет чистой приведенной стоимости уже учитывает такие факторы, как стоимость капитала инвестора, альтернативные издержки и устойчивость к риску через ставку дисконтирования. Кроме того, учитываются будущие денежные потоки проекта вместе с временной стоимостью денег. Следовательно, даже чистая приведенная стоимость в размере 1 доллара теоретически должна квалифицироваться как «хорошая», что указывает на то, что проект стоит того. На практике, поскольку оценки, используемые в расчетах, подвержены ошибкам, многие планировщики устанавливают более высокую планку для чистой приведенной стоимости, чтобы обеспечить себе дополнительный запас прочности.
Почему будущие денежные потоки дисконтируются?
NPV использует дисконтированные денежные потоки для учета временной стоимости денег. Пока процентные ставки положительны, доллар сегодня стоит больше, чем доллар завтра, потому что доллар сегодня может принести проценты за дополнительный день. Даже если будущие доходы можно спрогнозировать с уверенностью, их следует сбрасывать со счетов, поскольку должно пройти время, прежде чем они будут реализованы, — время, в течение которого сопоставимая сумма может приносить проценты.
Внутренняя норма доходности (IRR): определение, формула и пример
24 августа 2022 г.
Для оценки и ранжирования потенциальных инвестиционных возможностей и бизнес-проектов внутренняя норма доходности является одним из важных показателей, который предприятия и частные лица используют для финансового анализа.
В этой статье рассматриваются значение внутренней нормы доходности, формула IRR, способы расчета внутренней нормы доходности, когда она используется, а также часто задаваемые вопросы.
Содержание
Что такое внутренняя норма доходности (IRR)?
Понимание IRR
Формула внутренней нормы прибыли
Как рассчитать IRR
Когда (и зачем) использовать IRR?
Часто задаваемые вопросы
Что считается хорошей внутренней нормой доходности?
Что такое средняя внутренняя норма доходности 30%?
Что такое пример внутренней нормы доходности?
В чем разница между IRR и ROI?
Важность внутренней нормы прибыли
Что такое внутренняя норма прибыли (IRR)?
Внутренняя норма доходности — это расчет бюджета капиталовложений для принятия решения о том, какие проекты или инвестиции являются достойными инвестиций, и ранжирования их. IRR — это ставка дисконтирования, при которой чистая приведенная стоимость (NPV) равна нулю (когда будущие денежные потоки с поправкой на время равны первоначальным инвестициям). IRR — это показатель годовой доходности, который также используется для оценки фактической эффективности инвестиций.
Понимание IRR
IRR рассчитывается с использованием другого типа анализа дисконтированных денежных потоков для определения ставки, обеспечивающей безубыточность первоначальных инвестиций. Первоначальные инвестиции — это затраты компании на запуск инвестиционного проекта.
Предприятия сравнивают внутреннюю норму прибыли (IRR) потенциальных проектов. При оценке потенциальных вариантов инвестирования они часто выбирают самую высокую ожидаемую доходность IRR, которая соответствует минимальной пороговой ставке процента, необходимой для инвестиций компании, или превышает ее.
Если сумма бюджета достаточно велика для инвестирования более чем в один проект, то свободные средства распределяются на другие проекты с более высоким IRR в рамках бюджета компании и допустимого риска.
Базовый анализ денежных потоков — это анализ притока и оттока денежных средств, которые представлены в отчете о движении денежных средств.
Корпоративная пороговая ставка равна их средневзвешенной стоимости капитала (WACC), включая премию за риск. Согласно стратегическому финансовому директору, WACC компании представляет собой средневзвешенную стоимость собственного капитала, долга и привилегированных акций.
Статья Harvard Business Review о внутренней норме доходности (IRR) рекомендует использовать IRR в сочетании с чистой приведенной стоимостью (NPV) для принятия более эффективных инвестиционных решений. В финансовом анализе чистой приведенной стоимости положительная чистая приведенная стоимость означает рентабельность инвестиций.
В корпоративных финансах фирмы венчурного капитала и компании прямых инвестиций используют доходность наличными или внутреннюю норму доходности в качестве методов для анализа того, какие стартапы и растущие компании они должны финансировать в качестве портфельных инвестиций. Инвесторы в коммерческую недвижимость используют IRR для оценки потенциальной или фактической доходности инвестиционной недвижимости.
Физические лица также могут использовать IRR для осуществления личных инвестиций и принятия важных решений о покупках, которые могут приносить прибыль, например аннуитет.
Формула внутренней нормы прибыли
Формула внутренней нормы прибыли (IRR) основана на формуле чистой приведенной стоимости (NPV), когда она используется для расчета нулевой чистой приведенной стоимости.
Формула внутренней нормы доходности:
Как рассчитать IRR
Финансовые аналитики могут использовать математические формулы для расчета IRR методом проб и ошибок путем расчета чистой приведенной стоимости (NPV) каждой суммы денежного потока, используя оценку внутренней нормы доходности. По данным Journal of Accountancy, более эффективным процессом является использование трех функций электронных таблиц Excel для IRR, включая IRR, XIRR и MIRR.
Вместо этого вы можете использовать финансовый калькулятор для IRR. Финансовый калькулятор может быть либо физическим устройством с кнопкой IRR (например, специализированным финансовым калькулятором Texas Instruments), либо финансовым онлайн-калькулятором для внутренней нормы прибыли. Если вы решили использовать онлайн-калькулятор, сначала сравните результаты с Excel, чтобы убедиться в его точности.
Каждая формула функции Microsoft Excel имеет определенные встроенные предположения и переменные для вставки. Чтобы Excel работал при расчете трех функций IRR, ряд денежных потоков должен включать по крайней мере одну сумму отрицательного денежного потока для чистого оттока денежных средств и одну положительную сумму денежного потока для чистого притока денежных средств.
Функция IRR в Excel
Функция IRR в Excel предполагает периодические денежные потоки. IRR предполагает равное количество дней в месячных периодах движения денежных средств. Это не отражает ежемесячные колебания количества календарных дней в течение месяца, что приводит к небольшой неточности расчета IRR. В Excel для функции IRR вы можете вычислить IRR, используя либо месячные, либо годовые суммы, и выбрать, следует ли использовать предположение.
Расчет IRR за определенное количество лет (или месяцев). В функции IRR введите идентификаторы строки и столбца в виде суммы за годы, учитываемые при расчете IRR. Если вы делаете предположение, это дополнительная запись в формуле функции.
Шаги для использования функции Excel IRR:
Щелкните функцию f _x в Excel.
Выберите финансовую функцию.
В поле поиска функции введите IRR для функции IRR (и выберите IRR, если есть выбор, какую функцию IRR использовать).
Используя экран «Аргументы формулы», вставьте диапазон данных Excel в качестве значений для анализируемого периода внутренней нормы доходности и, при необходимости, свое предположение о величине внутренней нормы доходности.
В приведенном ниже разделе «Пример внутренней нормы доходности», который включает предположения о денежных потоках, Excel рассчитывает внутреннюю норму доходности как 16% на пятилетний период времени.
Функция ЧИСТВНДОХ в Excel
Функция ЧИСТВНДОХ в Excel не требует периодических денежных потоков и вместо этого использует даты денежных потоков (используя функцию ДАТА Excel или даты в ячейках Excel, отформатированных как ДАТА). Однако вы можете использовать периодические даты. Как и IRR, XIRR позволяет пользователю Excel дополнительно вставить предположение в экранное окно «Аргументы функции».
Шаги для использования функции ЧИСТНДОХ в Excel:
Щелкните функцию f _x в Excel.
Выберите финансовую функцию.
В поле поиска функции введите ЧИСТДДД для этого типа функции ВСД (или выберите ЧИСТДДД, если есть выбор, какую функцию ВСД использовать).
Используя экран «Аргументы формулы», вставьте диапазон данных Excel в качестве значений для анализируемого периода внутренней нормы доходности, введите диапазон ячеек даты, которые были отформатированы как ДАТА, и, необязательно, ваше предположение о ставке внутренней нормы доходности.
Используя те же предположения, что и в разделе «Пример внутренней нормы доходности» ниже, за исключением замены «Годы» фактическими датами поступления денежных средств, которые указаны в новом столбце C, ЧИСТВНР вычисляет ЧВНП как 14%.
Столбец C Excel содержит следующие даты и адреса ячеек, которые следует использовать в связи с Примером данных предположений IRR вместо номера года. Предполагается, что денежные потоки останутся прежними.
Cell Dates of Cash Flows Excel Cell Formatted as DATE
2-Jan-17 C2
15-Jan-18 C3
25 -19 марта C4
16-Feb-20 C5
22-May-21 C6
28-Dec-22 C7
The XIRR function calculation shows in Excel as XIRR(B2 :B7,C2:C7) или XIRR(B2:B7,C2:C7,. 11) с допущением 11%. Вычисленный ЧССНП отображается как 14%, и эти формулы появляются на панели содержимого ячейки в верхней части электронной таблицы Excel, если вы нажмете на результат 14%.
Функция MIRR в Excel
MIRR — это модифицированная внутренняя норма доходности. Функция MIRR в Excel использует периодические денежные потоки (как и функция IRR), а также предполагает реинвестирование денежных средств при расчете. Функция MIRR Excel включает в себя аргументы функций для значений, Finance_rate и Reinvest_rate, но не предполагает ожидаемого значения IRR. Финансовая_ставка — это процентная ставка, выплачиваемая по суммам, взятым взаймы для финансирования денежных потоков. Reinvest_rate — это процентная ставка для процентов, полученных, когда деньги реинвестируются из денежных потоков, полученных от инвестиционного проекта.
Шаги для использования функции MIRR Excel:
Щелкните функцию f _x в Excel.
Выберите финансовую функцию.
В поле поиска функции введите MIRR для этого типа функции IRR (или выберите MIRR, если есть выбор, какую функцию IRR использовать).
Используя экран «Аргументы формулы», вставьте диапазон данных Excel как «Значения денежных потоков за анализируемый период IRR» и введите «Finance_rate» и «Reinvest_rate».
Предположим, что Finance_rate равен 8%, а Reinvest_rate равен 12%. Используя те же предположения о денежных потоках и сроках, что и в разделе «Пример внутренней нормы доходности» ниже, функция Excel вычисляет MIRR как 15%.
Когда вы нажмете 15% для результатов функции MIRR, вы увидите MIRR(B2:B7,.08,.12) на панели содержимого ячейки Excel.
Когда (и зачем) использовать IRR?
Используйте IRR (внутреннюю норму доходности) для оценки и сравнения доходности бизнес-инвестиционных проектов, чтобы выбрать наилучшие инвестиции из этих конкурирующих проектов. Предприятия часто выбирают инвестиционные проекты с наивысшей доходностью в рамках своей склонности к риску, которая соответствует их минимальной пороговой ставке для инвестирования. Физические лица также могут использовать IRR для инвестирования.
Вы также можете использовать IRR для определения нормы прибыли на фактические инвестиции, когда чистая приведенная стоимость равна нулю, используя анализ дисконтированных денежных потоков.
Часто задаваемые вопросы
Ниже приведены ответы на часто задаваемые вопросы о внутренней норме доходности (IRR).
Что считается хорошей внутренней нормой доходности?
Хорошая IRR зависит от отрасли и рискованности проекта. Проекты с более высоким риском требуют большей доходности IRR. Предприятия выбирают проекты с внутренней нормой доходности, превышающей их минимальную пороговую доходность, которая равна или превышает средневзвешенную стоимость капитала (WACC). В сфере недвижимости хорошая IRR может варьироваться от 12% до 20%, в зависимости от уровня риска.
Что означает IRR 30%?
IRR в размере 30% означает, что норма прибыли на инвестиции с использованием прогнозируемых дисконтированных денежных потоков будет равна первоначальной сумме инвестиций, когда чистая приведенная стоимость (NPV) равна нулю. В этом случае, когда к денежным потокам применяются факторы временной стоимости денег, результирующая внутренняя норма доходности составляет 30%. Инвестиции находятся в безубыточности с 30% IRR.
Пример IRR?
Пример использования функции IRR в Excel включает следующие предположения:
Пороговая ставка в качестве необязательного предположения: 11%
WACC: 8%
Для периода в пять лет Excel показывает функцию IRR как:
IRR(B2:B7) без предположения IRR или IRR (B2:B7, .11) с предположением 11% для IRR.
Результат: Для приведенного выше примера IRR = 16%
В этом примере в течение пяти лет этот проект возвращает IRR в размере 16%, что превышает пороговую норму компании в 11% для минимального возврата инвестиций. Если это единственный рассматриваемый проект, выберите его. Если бизнес рассматривает другие инвестиционные проекты, ранжируйте их по наибольшей внутренней норме доходности выше пороговой ставки, но учитывайте и другие факторы, включая продолжительность бизнес-инвестиционного проекта, риск и требуемую сумму инвестиций.