Что такое осевая и центральная симметрия?
Поможем понять и полюбить математику
Начать учиться
263.8K
Осевая и центральная симметрия — тема для перфекционистов, любителей снимков в отражении и противников заваленного горизонта. Симметрично — значит красиво? Тогда давайте разберемся, что такое симметрия с точки зрения математики.
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
На рисунках осевая симметрия: точки A и B симметричны относительно прямой a; точки R и F симметричны относительно прямой AB
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
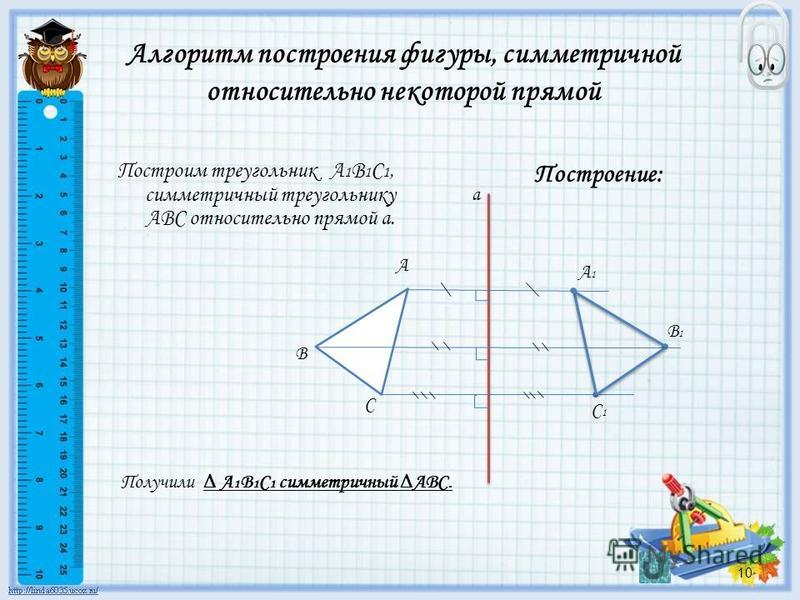
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1.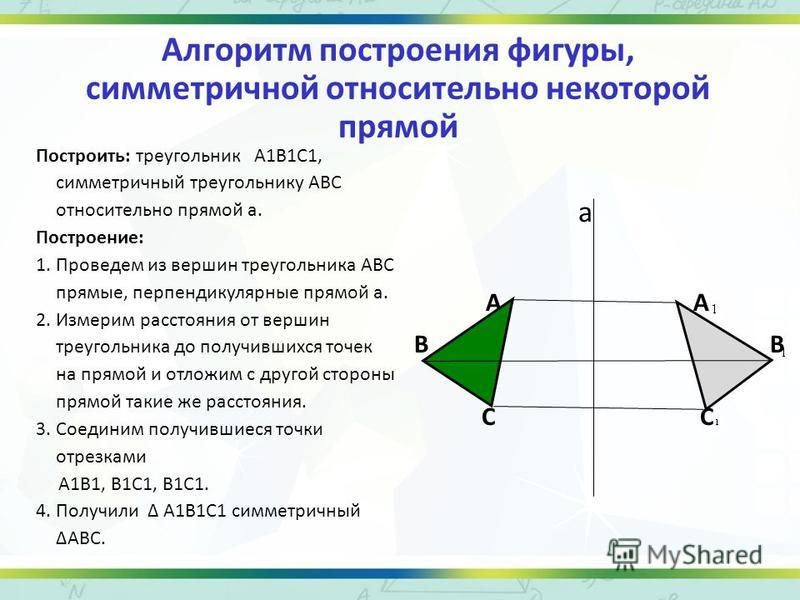 Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.

- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.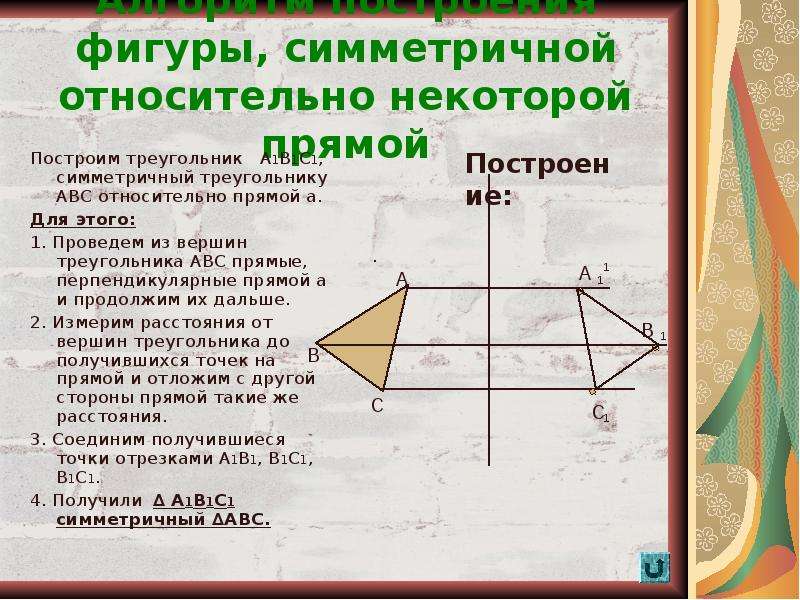
На картинках центральная симметрия: точка O здесь — центр симметрии
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.

- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно.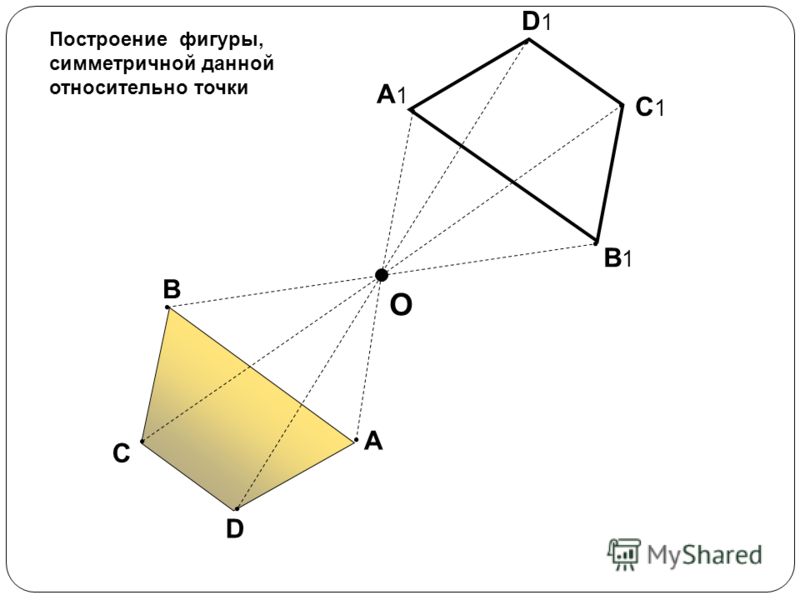
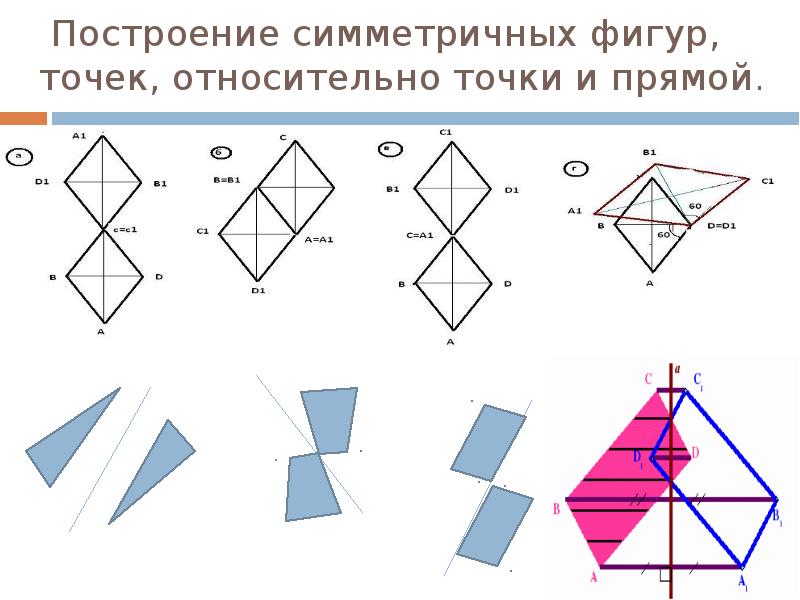
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
249.5K
Прямоугольный параллелепипед. Что это такое?
К следующей статье
129.7K
Как сокращать алгебраические дроби?
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
Коробку равномерно тянут по горизонтальной поверхности с помощью верёвки, составляющей с горизонтом угол 60°.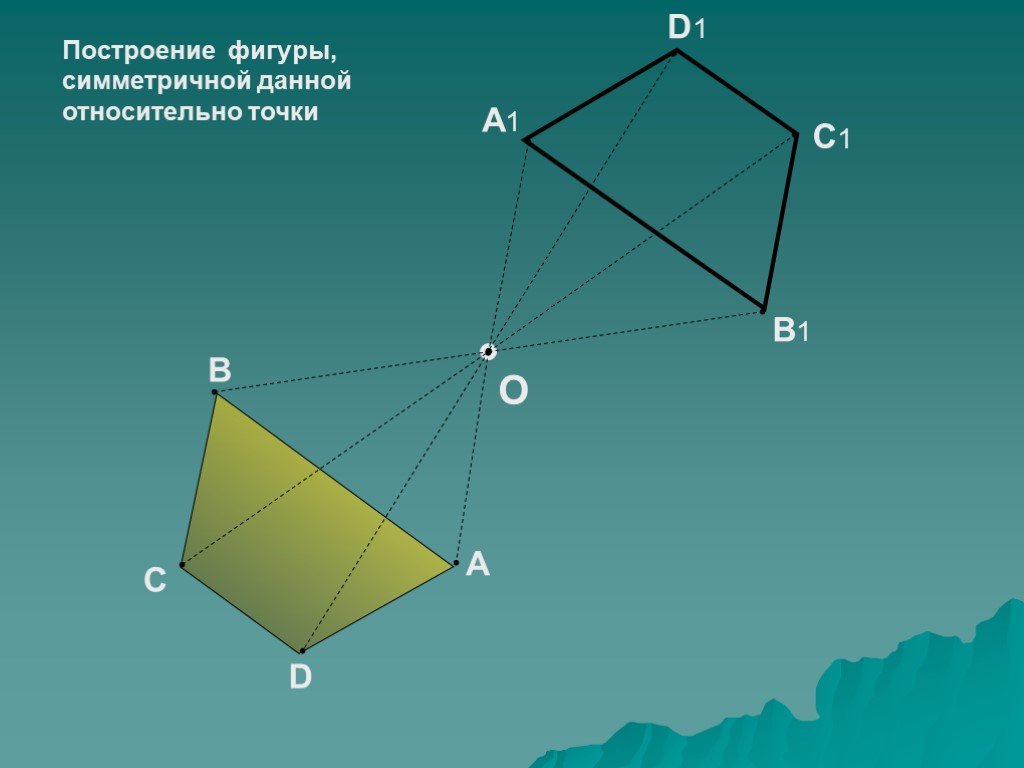 2-2x-8. Найдите с помощью графика :
a)Значение y при x = -1,5;
б) Значение х при которых у=3;
в) Нули функции;промежутки в которых у>0 и в которых у<0;
г)
2-2x-8. Найдите с помощью графика :
a)Значение y при x = -1,5;
б) Значение х при которых у=3;
в) Нули функции;промежутки в которых у>0 и в которых у<0;
г)
сокращенное ионное уравнение реакции Ba(2+) + SO4(2-) = BaSO4 соответствует взаимодействию
Пользуйтесь нашим приложением
Симметрия – Элементарная математика
Хотя существует много видов симметрии, в начальной школе обычно представлена только отражающая симметрия (или «зеркальная симметрия»). В результате в школьных материалах слово «симметрия» используется так, как если бы оно имело только одно значение. Эта статья сосредоточится на этом одном значении, но также проиллюстрирует и другие.
На этой фотографии показано простое изображение с зеркалом, расположенным вдоль линии симметрии. Результат, который вы видите — половина оригинала и зеркальное отражение этой половины — точно соответствует исходной фигуре. Мы говорим, что исходная фигура «симметрична» относительно зеркала; имеет отражательную симметрию.
Мы говорим, что исходная фигура «симметрична» относительно зеркала; имеет отражательную симметрию.
Отражающая симметрия и «линия симметрии»
Зеркально-симметричные объекты имеют по крайней мере одну линию симметрии , линию, по которой фигуру можно сложить на две точно совпадающие части, части, являющиеся зеркальным отображением каждой другой.
Эта фигура имеет две линии симметрии: горизонтальная линия симметрии делит фигуру на верх и низ, которые являются зеркальными отражениями друг друга; вертикальная линия симметрии разрезает фигуру на левую и правую части, которые являются зеркальными отражениями друг друга. Звезда внизу имеет 5 линий симметрии, пять линий, по которым ее можно сложить так, чтобы обе стороны идеально совпадали.
Распространенное заблуждение , встречающееся даже во многих словарях и текстах: не все линии, делящие фигуру на две конгруэнтные части, являются линиями симметрии. Например, диагональ (неквадратного) прямоугольника не является линией симметрии.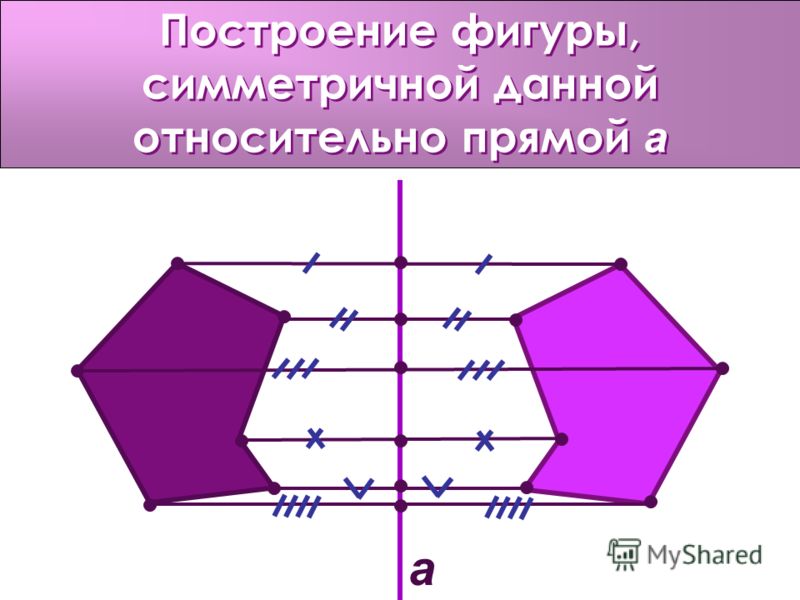
Когда зеркало помещается по диагонали прямоугольника, результат не выглядит так же, как исходный прямоугольник, поэтому диагональ не является линией симметрии. Эта новая форма — комбинация треугольной половины исходного прямоугольника и его отражения в зеркале — называется воздушным змеем.
Игра с зеркалом
Задолго до того, как дети начнут какое-либо формальное изучение симметрии, играя с зеркалами — возможно, с рисунками, которые они строят, — они развивают опыт и интуицию, которые могут служить как их геометрическому мышлению, так и их художественным идеям. Красочный дизайн выше имеет только вертикальные и горизонтальные линии симметрии, но размещение зеркала под другим углом может создать новый красивый дизайн.
На первом рисунке ниже видно, что буква А имеет вертикальную линию симметрии, но это скорее «ручная» игра. Более смелые эксперименты дают другие интересные результаты.
То же самое и с буквой M.
Буквы типа B и D имеют горизонтальную линию симметрии: их верхняя и нижняя части совпадают.
Некоторые буквы, например X, H и O, имеют как вертикальные, так и горизонтальные линии симметрии.
А некоторые, например P, R и N, не имеют линий симметрии.
Вращательная симметрия
Другая симметрия, которую дети иногда используют в своих рисунках из блоков узоров, называется «вращательная симметрия». Фигура обладает вращательной симметрией, если при некотором вращении (кроме полного поворота на 360 °) получается та же фигура. Например, эти фигуры при правильном вращении — 360°/3 для изображения «имя» и 360°/5 для звезды — выглядят точно так же, как и до поворота.
Буквы N, Z и S также обладают этим свойством.
Обратите внимание, что некоторые фигуры, такие как звезда и красочное пятно в верхней части страницы, но не буквы N, Z или S, имеют как отражательную, так и вращательную симметрию.
Самая симметричная фигура
Круг имеет бесконечно много линий симметрии: любой диаметр лежит на линии симметрии, проходящей через центр круга. Любое вращение на любую величину вокруг центра круга также оставляет круг неизменным.
Любое вращение на любую величину вокруг центра круга также оставляет круг неизменным.
Книги для детей
- Для детей младшего возраста, К-2:
- Сделай лужу побольше Сделай червяка поменьше , Марион Уолтер
- Для детей старшего возраста, 2 класс и старше:
- Книга-головоломка с зеркалом , Марион Уолтер
Что в слове?
«Метрика» в симметрия и геометрия и метрика относится к измерению.
Симметрия: определение, типы, упражнения и примеры
Сегодня вы узнаете, что такое симметрия, и мы увидим некоторые упражнения на симметрию, которые дети выполняют во время занятий Smartick, и типичные ошибки, которые обычно делаются.
Что такое симметрия?
Симметрия — это одна из математических концепций, которую учащиеся начинают изучать вне школы. Тем не менее, они все еще изучают его в дошкольном образовании и строят симметричные фигуры, не используя строгого определения.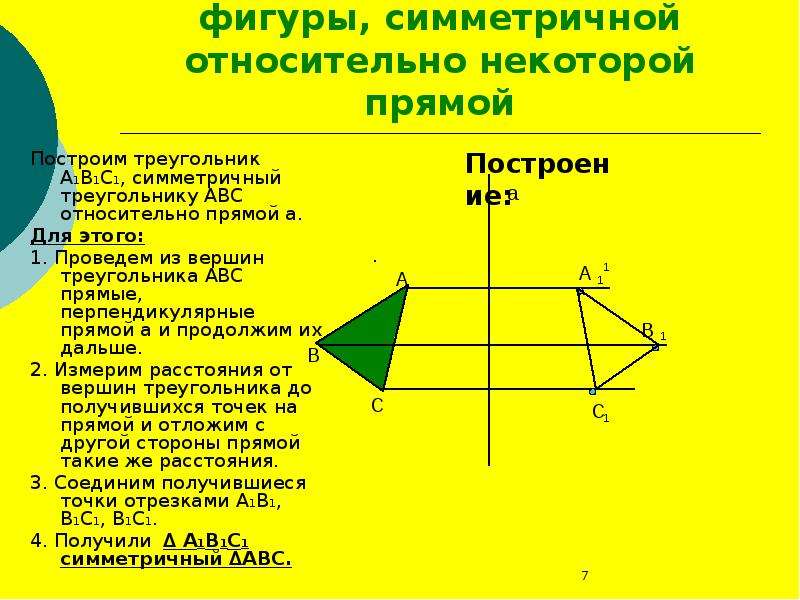
Как мы увидим ниже, существуют различные типы симметрии. Начнем с самых известных, симметрия относительно прямой или осевая симметрия . Давайте начнем с рисования прямой линии на плоскости, в данном случае это может быть лист бумаги с сеткой, как показано на рисунке ниже:
Линия нарисована вертикально, но она может быть горизонтальной или иметь любое другое направление.Мы говорим, что фигура симметрична относительно прямой, если каждая точка на одной стороне этой прямой имеет другую точку на другой стороне и на том же расстоянии от этой прямой.
Если мы хотим узнать, симметрично ли изображение относительно линии и есть ли оно на листе бумаги, нам просто нужно согнуть лист вдоль линии. Если при сгибании листа фигуры совпадают друг с другом, то это потому, что они симметричны относительно линии. Если они не совпадают, то они несимметричны.
Если мы хотим создать симметричное изображение на бумаге, мы начинаем с складывания бумаги и, используя маркер, который будет слегка просвечивать бумагу, рисуем желаемую фигуру.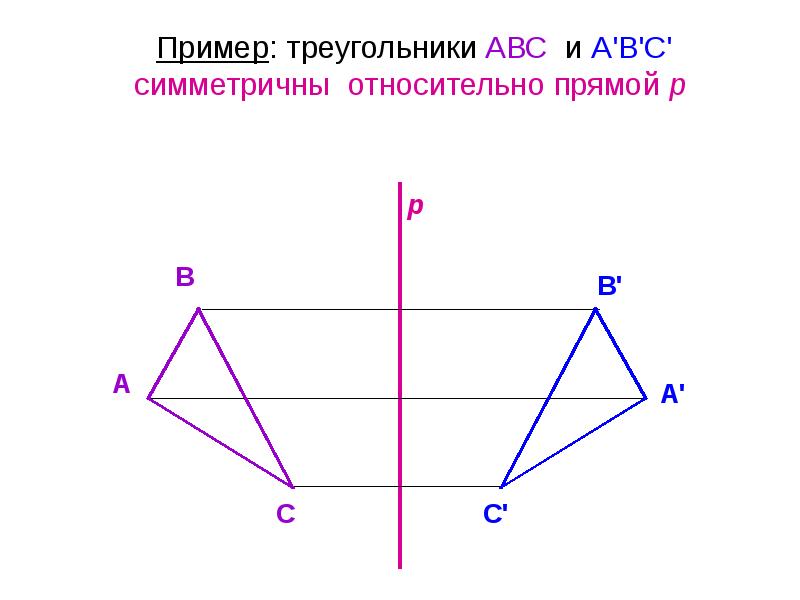 Затем разворачиваем бумагу. Маркер перетек на другую сторону и создал две фигуры, симметричные относительно линии, которую мы сложили. Когда лист сложен, они точно совпадают. Мы также могли бы использовать ножницы вместо маркера.
Затем разворачиваем бумагу. Маркер перетек на другую сторону и создал две фигуры, симметричные относительно линии, которую мы сложили. Когда лист сложен, они точно совпадают. Мы также могли бы использовать ножницы вместо маркера.
Видео: Симметричные фигуры и оси симметрии
Чтобы лучше понять, что такое симметрия с по отношению к оси , посмотрите это видео одного из наших интерактивных руководств. Он больше не интерактивный, но у вас есть преимущество в том, что вы можете смотреть его столько раз, сколько необходимо, и делиться им с другими. Если вы хотите получить доступ к реальным интерактивным урокам, зарегистрируйтесь в Smartick, онлайн-методе обучения математике для детей в возрасте от 4 до 14 лет.
В этом видео мы представляем мастер-класс по симметрии, посмотрите:
Что такое ось симметрии?
Симметричная фигура может иметь одну или несколько осей симметрии, которые могут быть прямыми линиями или линиями, делящими фигуру на две симметричные части.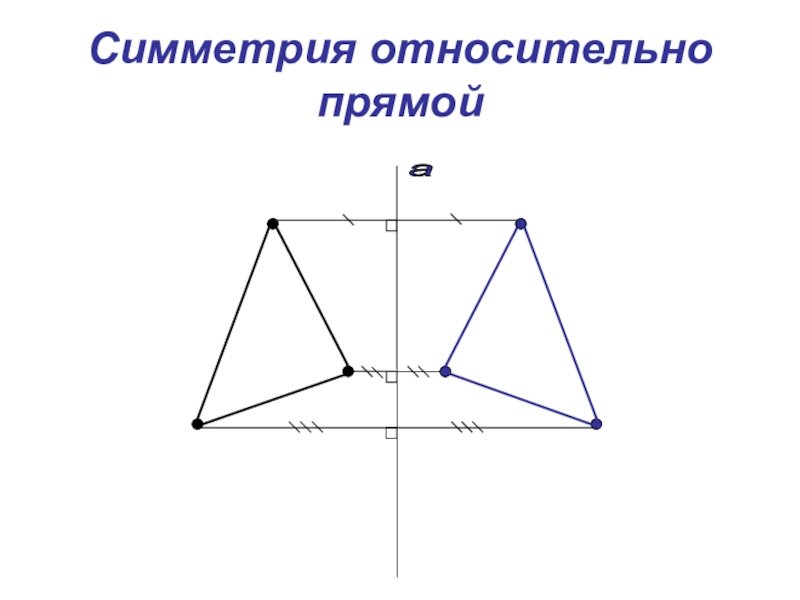
На изображении, взятом из видео, у звезды четыре оси симметрии, а у рук только одна – вертикальная прямая.
Типы симметрии
Существует много типов симметрии, но мы сосредоточимся на этих трех, которые можно увидеть в школе:
- Во-первых, осевая симметрия, или симметрия относительно линии, — это та, которая делит объект или фигуру пополам с помощью прямой линии , другими словами, по оси симметрии. Этот тип симметрии может напоминать ситуацию, когда мы смотрим в зеркало и видим в нем свое отражение.
- Мы говорим, что одна или несколько фигур имеют вращательную симметрию , когда они не изменяются при повороте на определенный угол. Четырехконечная звезда на предыдущем изображении обладает вращательной симметрией, потому что если вы повернете ее на 90º (или любой кратный 90º) будет то же самое.
- Третий тип симметрии, встречающийся на плоскости, — это симметрия относительно точки или центральная симметрия .
 Две точки симметричны относительно точки, которую мы называем центром симметрии, если они находятся на одинаковом расстоянии от нее и на одной линии. Центральная симметрия производит тот же эффект, что и поворот на 180º.
Две точки симметричны относительно точки, которую мы называем центром симметрии, если они находятся на одинаковом расстоянии от нее и на одной линии. Центральная симметрия производит тот же эффект, что и поворот на 180º.
Упражнения на симметрию в Smartick
В посте о новом контенте Smartick мы привели примеры последовательности действий на симметрию. Сложность зависит от формы фигур и ориентации оси симметрии. Сложность постепенно увеличивается, мало-помалу, облегчая изучение и понимание этой концепции. Эти упражнения способствуют развитию пространственного зрения и геометрического мышления.
- У нас есть упражнения, в которых дети должны проанализировать, симметричны ли две фигуры:
- В других они должны построить симметричные фигуры:
- Или расположите ряд точек симметрично на наклонной оси:
Типичные ошибки
Эти две фигуры симметричны относительно оси? Студенты часто допускают две ошибки, когда сталкиваются с этим вопросом.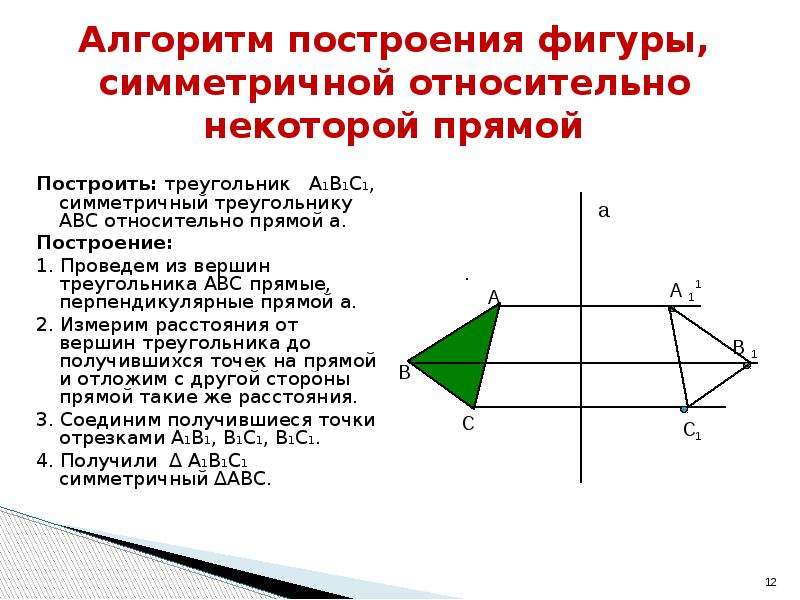
- Подумайте, одинаковы ли фигуры, если они симметричны:
Чтобы исправить эту ошибку (как мы упоминали ранее), полезно думать о сетке как о бумаге, которую можно согнуть по оси симметрии. Если в сложенном виде фигуры не совпадают, то это потому, что они несимметричны. Другой способ — думать об оси как о зеркале, если одна фигура не является отражением фигуры, которая будет проецироваться в зеркало, то они не симметричны.
- Другая распространенная ошибка — думать, что если одна фигура является зеркальным отражением другой, то они симметричны независимо от их положения относительно оси симметрии:
Мы можем использовать те же стратегии, что и раньше, чтобы устранить эту ошибку. Если мы согнем бумагу по оси симметрии, то фигуры не совпадут. И одна фигура не является отражением другой в осевом зеркале.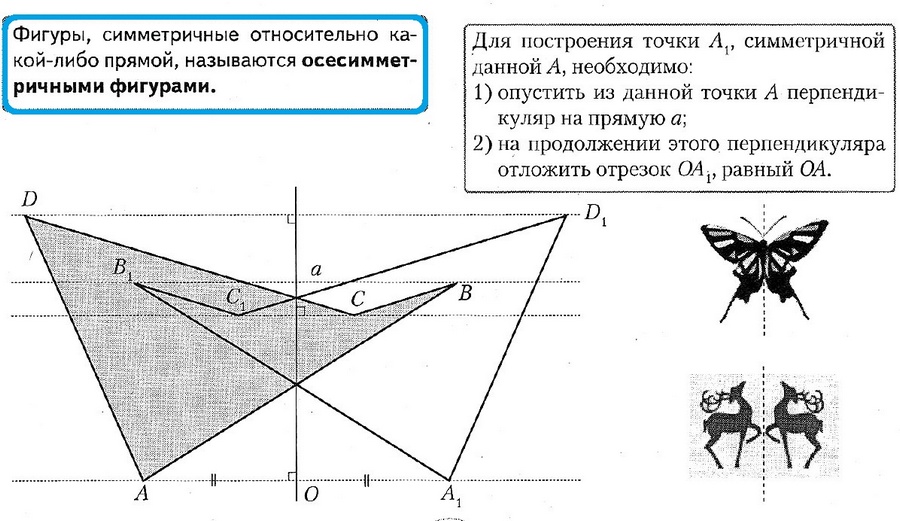 Следовательно, эти две фигуры несимметричны относительно оси.
Следовательно, эти две фигуры несимметричны относительно оси.
Симметрия вне математики
Симметрия вокруг нас:
- В зеркале или отражении на поверхности воды. Отраженное изображение симметрично реальному изображению.
- В нас самих: у нас есть правая рука и левая рука, правое ухо и левое ухо, и каждая пара симметрична. Наше тело разделено на две симметричные части, правую и левую, относительно оси, проходящей от макушки головы до пальцев ног.
- Фасады большинства домов и зданий симметричны относительно вертикальной оси.
- Машины, тостеры, сотовые телефоны, стакан, тарелка, бутылка, телевизор, диван… Большинство повседневных предметов имеют одну или несколько осей симметрии.
- Мы также можем найти симметрию в искусстве. Художники используют симметрию в живописи, скульптуре, музыке и многих других дисциплинах.
- В природе тоже. Большинство животных и растений имеют тот или иной тип симметрии: двустороннюю, радиальную…
Если вы хотите больше узнать о геометрии и математике в начальной школе, зарегистрируйтесь в Smartick и попробуйте бесплатно.


 11.21
11.21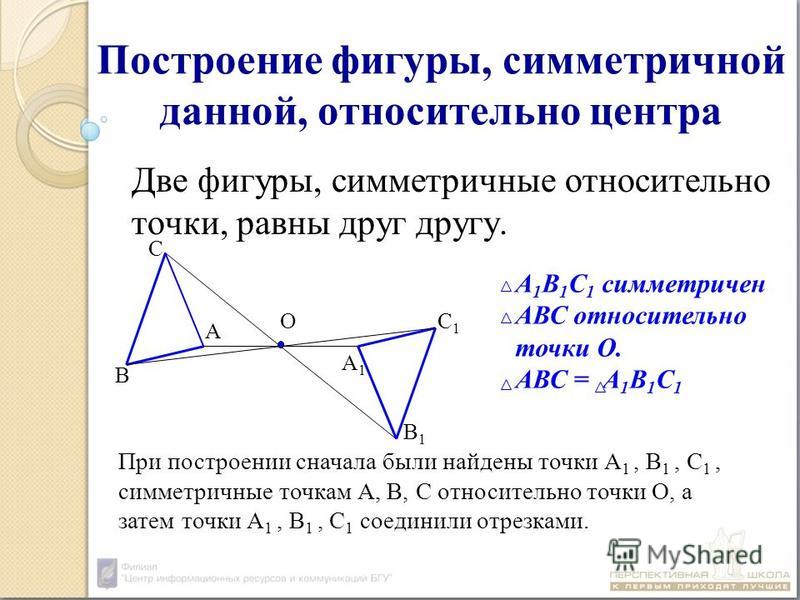 Две точки симметричны относительно точки, которую мы называем центром симметрии, если они находятся на одинаковом расстоянии от нее и на одной линии. Центральная симметрия производит тот же эффект, что и поворот на 180º.
Две точки симметричны относительно точки, которую мы называем центром симметрии, если они находятся на одинаковом расстоянии от нее и на одной линии. Центральная симметрия производит тот же эффект, что и поворот на 180º.