Фактор в факторинге: что это простыми словами, примеры, виды

Содержание

Глоссарий / Ассоциация Факторинговых Компаний

Андеррайтинг

— сбор и анализ информации (проверка бизнес репутации покупателя, проверка аффилированности между клиентом и дебитором, анализ финансового состояния дебитора и установление лимитов финансирования).

Аутсорсинг

— передача части работ на исполнение сторонней организации.

АФК

— Некоммерческая организация «Ассоциация факторинговых компаний» созданная в целях развития факторингового бизнеса в Российской Федерации, объединяющая на добровольной основе организации, прямо или косвенно имеющие отношение к факторингу;

Верификация

— комплекс мер, направленных на выявление недействительной дебиторской задолженности, а также других фактов, препятствующих добросовестному исполнению сторонами своих обязательств по договору.

Дебитор (Дебиторы)

— юридическое лицо или Индивидуальный Предприниматель (резидент РФ или нерезидент), осуществляющий предпринимательскую деятельность и выступающий в качестве покупателя по Контракту, заключенному с Клиентом.

Денежные требования

— требования Клиента об уплате Дебитором денежной суммы в оплату отгруженных товаров, выполненных работ или оказанных услуг в соответствии с Контрактом.

Импорт-Фактор

— иностранная факторинговая компания, которой Поручитель может поручить представлять свои интересы, в т.ч. оказывать услуги по управлению кредитным риском Дебиторов.

Клиент

— юридическое лицо или физическое лицо, ведущее предпринимательскую деятельность без образования юридического лица (индивидуальный предприниматель или глава крестьянского (фермерского) хозяйства, заключившее договор об оказании услуг по факторинговому обслуживанию).

Коллекторские услуги

— комплексные услуги по возврату задолженностей физических лиц.

Контракт

— договор купли-продажи товаров, выполнения работ или оказания услуг, заключенный между Клиентом и Дебитором.

Контрактный лимит Дебитора

— устанавливаемая Фактором максимальная сумма денежных требований Клиента к Дебитору, которая определяется Фактором как размер допустимого риска по поставкам в адрес конкретного Дебитора.

Кредитный риск

— риск полной или частичной неоплаты Дебитором сумм дебиторской задолженности, а также длительная просрочка, определяемая согласно договору.

Основное обязательство

— обязательство Дебитора оплатить поставленные Клиентом товары/оказанные Клиентом услуги в рамках Контракта.

Поручительство

— обязательство Поручителя исполнить каждое из Основных обязательств Дебитора в случае неисполнения этого обязательства Дебитором в соответствии с условиями настоящего Договора.

Поставка

— поставка Клиентом Дебитору товаров, оказание услуг или выполнение работ, вследствие чего у Клиента к Дебитору возникает денежное требование.

Предельный размер финансирования денежного требования

— максимальный размер финансирования, выплачиваемый Фактором по конкретному уступленному денежному требованию, устанавливаемый в проценте (%) от суммы уступленного денежного требования.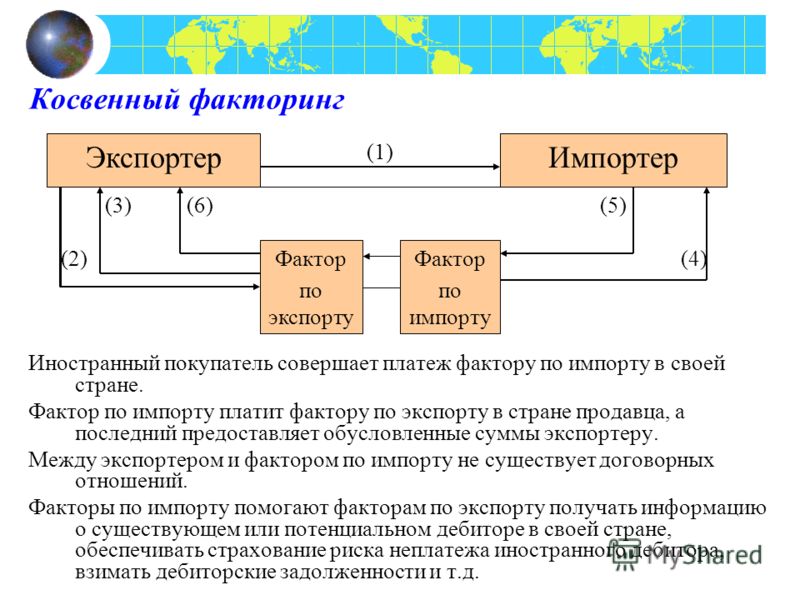

Регресс (а также в сочетаниях «факторинг с регрессом», «право регресса»)

— операции факторинга, при которых Фактор, не принимает на себя кредитные риски и имеет право требовать с Клиента возмещения любых раннее уплаченных Клиенту сумм финансирования в случаях оговоренных далее в тексте Договора или Дополнительного соглашения.

Рынок факторинга

— совокупность финансовых агентов, клиентов, регулирующих органов, коммерческих и некоммерческих организаций и отношений между ними, прямо или косвенно связанных с осуществлением факторинговой деятельности.

Уступка денежных требований

— уступка Продавцом существующих и/или будущих денежных прав требования к Дебитору Фактору НФК, в обеспечение выплаченного финансирования.

Фактор

— специализированная факторинговая компания или коммерческий банк, предоставляющий услуги факторинга.

Факторинг

— комплекс финансовых услуг, включающий полностью или по отдельности следующие составляющие: финансирование оборотного капитала, покрытие кредитного риска, учет дебиторской задолженности и сбор дебиторской задолженности. При этом факторингом может называться только деятельность, сочетающая не менее двух указанных составляющих. Финансирование оборотного капитала в рамках факторинга является разновидностью финансирования, обеспеченного активами (Asset Based Lending).

Факторинговое вознаграждение

— совокупный доход Фактора, включающий в себя все виды комиссий, штрафы, пени и другие виды вознаграждений за осуществление факторинговых операций.

Финансирование — денежные средства, предоставляемые Фактором Клиенту по передаваемым Клиентом поставкам на срок указанный в Дополнительном соглашении, на условиях срочности, платности и возвратности.

Подключить электронный факторинг с компанией КСК Фактор

О факторе

КСК Фактор — факторинговая компания, работает на рынке финансовых и консалтинговых услуг с 2010 года.

КСК-Фактор предлагает различные виды факторинга как для поставщиков, так и для покупателей. Размер финансирования при регрессном факторинге доходит до 100% от уступаемых прав требования.

8 800 777 78 01

Как работать

1

Заключите договор

Подпишите комплект документов в электронном виде и получите доступ к платформе

2

Создайте заявку

Выберите поставки, по которым вы хотите получить факторинговое финансирование

3

Отправьте фактору

Легко создайте запрос на проведение сделки по уступке дебиторской задолженности

4

Получите деньги

Дождитесь одобрения со стороны фактора и получите средства на расчётный счёт вашей компании.

Что понадобится

Электронная подпись
Доступ в интернет

Документы по поставкам

Форматы работы

Веб-доступ

Достаточно интернет-браузера и электронной подписи для быстрого начала работы

Интеграция

Соединим платформу с вашими внутренними системами через облегченную интеграцию

Дополнительно

Услуги оператора ЭДО

Подключим к электронному документообороту через Ediweb. Предложим выгодные тарифы и индивидуальные условия.

Персональная поддержка

Выделим специалистов, дистанционно помогающих с работой на FactorPlat.

Обучим сотрудников и обеспечим инструкциями.

Автоматизация

Избавим от необходимости проводить ручные операции по вводу данных на платформу.

Переходите на электронный факторинг сегодня вместе с FactorPlat

Свяжитесь с нашими специалистами, мы ответим на все вопросы по подключению

Ваша роль

Возможности

Отрасли

О компании

Учебник по алгебре среднего уровня 27

Алгебра среднего уровня
Урок 27: GCF и факторинг по группировке

WTAMU > Виртуальный Лаборатория математики > Алгебра среднего уровня

Цели обучения

После завершения этого руководства вы сможете:

Найдите наибольший общий делитель (НОД) многочлена.
Вынесите на множители GCF полинома.
Фактор многочлена с четырьмя членами путем группировки.

Введение

Факторинг заключается в написании выражения как произведения факторы. Например, мы можем записать 10 как (5)(2), где 5 и 2 называются факторы из 10. Мы также можем сделать это с полиномиальными выражениями. В В этом уроке мы рассмотрим два способа разложения полинома на множители. выражения, выделение наибольшего общего делителя и разложение на множители группировка. В следующих двух уроках мы добавим другие типы факторинг. Что-то, чтобы с нетерпением ждать! К тому времени, когда я закончу с ты, вы будете факторинговой машиной.

Другие будут спрашивать ты за помощь в факторинге.

В основном, когда мы факторизуем, мы обращаем процесс умножения полином, рассмотренный в Уроке 26: Умножение Полиномы.

Учебник

Наибольший общий делитель (GCF)

GCF для полинома является наибольшим мономом что делит (есть множитель) каждого члена многочлена.

Пример 1 : Найти GCF списка мономов:

Нам нужно выяснить, какой самый большой моном мы может разделить из каждого из этих терминов будет. Обратите внимание, что все они имеют

х , так что похоже, что будет задействовано x .

Показатели на x это 8, 7 и 6. Мы должны решить, какой показатель мы будем использовать. Если мы используем в показатель 8, у нас проблемы. Мы не можем делить или на , у нас недостаточно x для выполнения что. Но, если мы используем , у нас был бы моном, который мы могли бы разделить на ВСЕ термины.

Следовательно, наш GCF равен .

Обратите внимание, что если все термины имеют та же переменная, GCF для переменной части — это переменная, поднятая до самого низкого уровня. экспонента что указано.

Пример 2 : Найдите GCF списка мономов:

Нам нужно выяснить, какой самый большой моном мы может разделить из каждого из этих терминов будет. Что вы думаете?

Давайте сначала посмотрим на числовую часть. У нас есть 3, 9 и 18. Наибольшее число, которое можно разделить на эти числа, равно 3.

Таким образом, наш числовой GCF равен 3.

Теперь о переменной части. Похоже, каждый term имеет размеры x и y . В обоих случаях самая низкая экспонента равно 1.

Таким образом, GCF нашей переменной части равен xy .

Соединив это вместе, мы получим GCF 3 xy .

Факторизация GCF

Шаг 1. Определите GCF полинома.

Шаг 2: Разделите GCF из каждого термина полинома.

Этот процесс в основном противоположен дистрибутиву . свойство найдено в Уроке 5: Свойства действительных чисел.

Пример 3 : Вычтите GCF:

Шаг 1. Определите GCF полинома.

Самый большой моном, который мы можем вынести из каждого срок 2 х .

Шаг 2. Разделите GCF на каждый срок многочлен.

*Разделить 2 x из каждого члена поли.

Будьте осторожны. Если термин полинома точно такой же, как GCF, когда вы делите его на GCF, вы левый с 1, НЕ 0. Не думайте: «О, у меня ничего не осталось», на самом деле есть 1. Как показано выше, когда мы делим 2 x на 2 x , мы получаем 1, поэтому нам нужна 1 в качестве третий термин внутри ( ).

Обратите внимание, что если мы умножим наш ответ, мы должны получить оригинал многочлен. В этом случае он проверяется. Факторинг дает вам другой способ написать выражение, чтобы оно было эквивалентно оригинальная проблема.

Пример 4 : Вычтите GCF:

Шаг 1. Определите GCF полинома.

Самый большой моном, который мы можем вынести из каждого срок.

Шаг 2. Разделите GCF на каждый срок многочлен .

*Разделить каждый член многоугольника.

Обратите внимание: если мы умножим наш ответ, мы получим исходный многочлен.

Пример 5 : Вычтите GCF:

Эта задача выглядит несколько иначе, потому что теперь наша GCF является биномом.

Это нормально, мы относимся к этому так же, как когда у нас есть одночлен ЗКФ.

Обратите внимание, что это не в факторизованной форме из-за знак минус мы есть перед 7 в проблеме. Чтобы быть в факторизованной форме, он должен записать в виде произведения множителей.

Шаг 1. Определите GCF полинома.

На этот раз это не моном, а бином, который мы иметь общее.

Наш GCF равен (x + 5).

Шаг 2. Разделите GCF на каждый срок многочлен .

*Разделить ( x + 5) обе части

Когда мы разделим ( х + 5) из первого члена, у нас осталось x в квадрате. Когда мы разделим его на второй член, у нас останется -7.

Вот как мы получаем для нашего второго ( ).

Факторизация многочлена с
Четыре члена путем группировки

В некоторых случаях не существует GCF для ВСЕХ терминов в полиноме. Если у вас есть четыре термина без GCF, попробуйте разложить по группам.

Шаг 1: Сгруппируйте первые два термина вместе, а затем последние два термина вместе.

Шаг 2: Вынесите GCF из каждого отдельный бином.

Шаг 3: Вынесите за скобки общие биномиальный.

Пример 6 : Фактор по группировке:

Обратите внимание, что GCF не существует для ВСЕХ терминов. Так вперед и фактор это путем группировки.

Шаг 1: Сгруппируйте первые два термина вместе, а затем последние два термина вместе.

*Две группы по два термина

Шаг 2. Вынесите GCF из каждого отдельный бином.

*Вычтите квадрат x с 1-го ( )
*Вычтите 2 из 2-го ( )

Шаг 3: Вынесите за скобки общие биномиальный.

*Разделить ( x + 7) обе части

Обратите внимание: если мы умножим наш ответ, мы получим исходный многочлен.

Пример 7 : Фактор по группировке:

Обратите внимание, что GCF не существует для ВСЕХ терминов. Так вперед и фактор это путем группировки.

Шаг 1: Сгруппируйте первые два термина вместе, а затем последние два термина вместе.

*Две группы по два термина

Будьте осторожны. Когда первый член второго группа из двух человек знак минус перед ним, вы хотите поставить минус перед второй ( ). Когда вы это сделаете, вам нужно изменить знак обоих членов второго ( ), как показано выше.

Шаг 2. Вынесите GCF из каждого отдельный бином.

*Вычтите x из 1-й ( )
*Вычтите 4 из 2-го ( )

Шаг 3: Вынесите за скобки общие биномиальный.

*Разделить (3 x + y ) из обеих частей

Обратите внимание: если мы умножим наш ответ, мы получим оригинал многочлен.

Практические задачи

Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как что-либо иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться это. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.

Чтобы получить максимальную отдачу от этого, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

Практика Задачи 1а — 1г: Фактор.

1а.
(ответ/обсуждение к 1а)

1б.
(ответ/обсуждение к 1б)

1в.
(ответ/обсуждение к 1с)

1д.
(ответ/обсуждение до 1d)

Нужна дополнительная помощь по этим темам?

Следующие веб-страницы что может помочь вы в темах, которые были затронуты на этой странице:

http://www. purplemath.com/modules/simpfact.htm
Эта веб-страница поможет вам выделить GCF.

http://www.mathpower.com/tut111.htm
Эта веб-страница поможет вам с факторингом GCF.

Перейти к получению Помощь за пределами Классная комната в Учебнике 1: Как добиться успеха на уроке математики для некоторый больше предложений.

WTAMU > Виртуальная математическая лаборатория > Промежуточная алгебра

1.3 Методы факторинга. Методы исчисления 1

Методы факторизации

В этом разделе мы рассмотрим три шага факторизации многочлена: 92 + бх + с[/латекс]

Эти шаги факторинга часто используются как часть метода решения полиномиальных уравнений. 2 + 14x[/латекс] 92 + 14x = 2x(3x + 7)[/latex]

Разложение наибольшего общего делителя (GCF)

Выражение «[latex]2x[/latex]» называется наибольшим общим делителем (GCF).

Первым шагом в любой попытке факторинга является определение наличия наибольшего общего множителя. Чтобы определить наибольший общий множитель, разбейте его на два шага:

Изучите коэффициенты полинома и определите наибольшее целое число, которое равномерно делится на все коэффициенты. 92[/latex]
Решение:
Выполните следующие действия:
Изучите коэффициенты полинома и найдите наибольшее целое число, которое без остатка делится на все коэффициенты. Обратите внимание, что «9» — это наибольшее целое число, которое без остатка делится как на 27, так и на 36.
Просмотрите переменные выражения и определите наибольшее выражение, которое равномерно делится на переменные выражения в полиноме. Примечание. Переменная часть наибольшего общего делителя всегда содержит наименьшую степень переменной, которая входит во все члены многочлена.

Глоссарий / Ассоциация Факторинговых Компаний